El sonido es aire vibrando. Los instrumentos tradicionales se usan para vibrar el aire a frecuencias especificas. Se puede hacer esto con por ej.: cuerdas (violín), labios (trompeta), o membrana (timbal). Inclusive nosotros tenemos una membrana en el oído – el tímpano – que vibra al son de las vibraciones del aire. Nuestro cerebro transforma estas vibraciones en otra cosa, que es lo que llamamos sonido.

En música electrónica, usamos parlantes para generar sonido. Estos también tienen una membrana (o varias) que vibra, hacia adelante y hacia atrás, causando que el aire vibre.

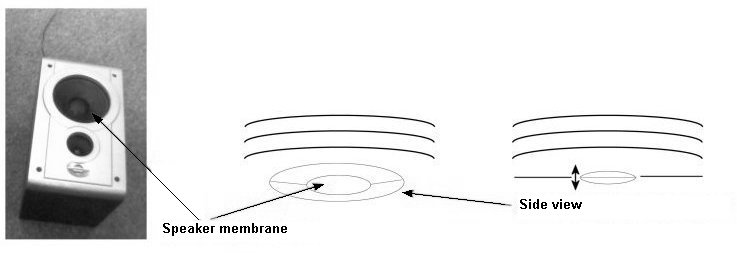
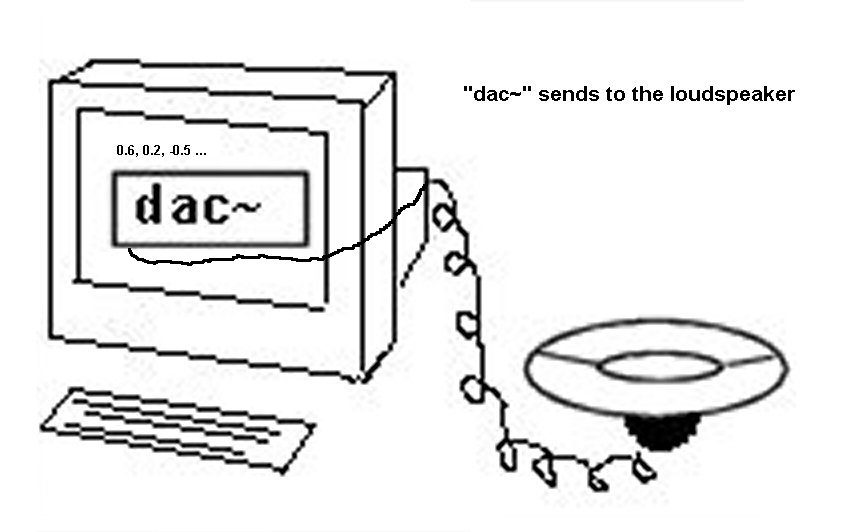
Las vibraciones de esta membrana son controladas por la computadora. En Pd, el objeto “dac~” (digital-to-analog converter) maneja esto. Funciona así: el sonido es un fenómeno físico – vibraciones en el aire para ser precisos – y como tales, son análogas. Las computadoras solo trabajan con números, Lo que significa que son digitales. El objeto “dac~”convierte los números en sonido convirtiendo los números en fluctuaciones de corriente eléctrica que, después de amplificadas, causan que la membrana(s) del parlante vibre correspondientemente.

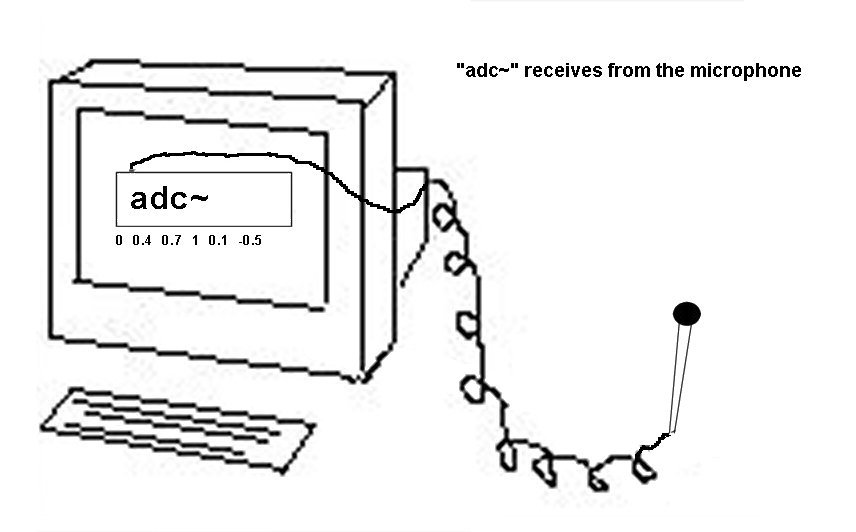
El proceso inverso se da cuando conectamos un micrófono a la computadora. El micrófono también tiene una membrana que responde a las vibraciones del aire y las convierte en fluctuaciones de corriente eléctrica , que es enviada a la computadora donde luego son convertidas en números. En Pd esta entrada se recibe con el objeto “adc~”(analog-to-digital converter).

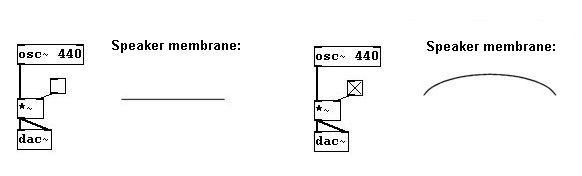
Volvamos a los parlantes por un momento. La membrana del parlante puede moverse hacia adelante o haca atrás. La posición mas hacia adelante (la mas convexa) es entendida por la computadora como posición 1. La posición mas hacia atrás (la mas cóncava) es posición -1. Cuando la membrana esta en el medio, o descanso, es la posicion 0. Todas las otras posiciones son valores entre -1 y 1.

En la realidad, estos movimientos son tan pequeños y tan rápidos que no se pueden observar a simple vista.

---

Imaginemos que una membrana se mueve desde un limite extremo hacia el otro (mas convexo, mas cóncavo) en un tempo constante:

Marquemos posiciones individuales:

De forma abstracta, con la posición de la membrana como eje “y” y el tiempo como eje “x”, podemos representar el movimiento así:

En términos físicos, esto es llamado onda. Aquí claramente se ve una forma de onda – una triangulo.

Hay diferentes formas de onda para diferentes tipos de movimientos de membrana. Sus nombres derivan de su parecido visual:

El objeto “osc~” del Pd crea una onda sinusoidal (sine).

Algo importante para recordar con respecto a las formas de onda: se repiten constantemente sin modificar sus características motrices. Las vibraciones que exhiban esta cualidad se denominan periódicas. Un periodo es un ciclo completo de la vibración que se repite constantemente.

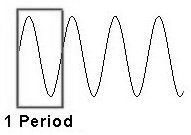
Lo que hace especial a las vibraciones periódicas es que las escuchamos claramente como tonos a una definida altura. Por el contrario los ruidos son vibraciones aperiódicas.

---

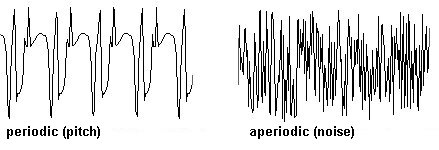
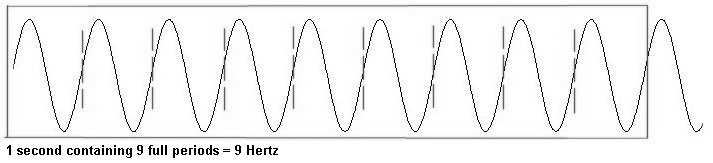
Veamos primero las vibraciones periódicas. Es posible, simplemente, contar la cantidad de periodos en un segundo. Este numero es la frecuencia de las vibraciones en “Hertz” (Hz); la frecuencia en este contexto siempre significa cuanto algo se repite en un segundo (expresado matemáticamente: 1/segundo).

La frecuencia, en un tono, determina su altura. A440 (la 440, también llamada A4, el tono standard de afinación que utilizan las orquestas) significa que el aire vibra periódicamente 440 veces por segundo. C5 (do 5) vibra 523 veces por segundo; el sol grave de un cello vibra casi 100 veces por segundo.

Aquí se puede ver que: cuanto mas lenta es la frecuencia, mas grave el tono es a nuestros oídos. De hecho los humanos, dependiendo de la edad, escuchamos frecuencias entre 20 Hz y 15000 Hz. Los niños hasta 20000; los ancianos a menudo solo hasta 10000 Hz. Los perros y murciélagos mucho mas de 20000 Hz. Este rango se denomina ultrasonico. En contraste con este esta el rango infrasonico, que esta por debajo del umbral audible, entre 0 y 20 Hz. Este rango es percibido por nosotros como ritmo. Puede usar el Pd para hacer una experiencia propia con el siguiente experimento:

Escuchara un ritmo de clicks (ese es el sonido de una onda serrucho) que gradualmente se hace mas rápido. Luego de determinada velocidad (mas de 20 clicks por segundo), nuestra percepción “pasa un cambio” y comenzamos a escuchar un tono grave. Para el aire (y la computadora) esto todavía es un “ritmo”. Pero para el oído humano ( a partir de 20 Hz) es un tono. Cuanto mas rápido es el ritmo, mas agudo es el tono que escuchamos.

Otra característica definitoria del oído humano es que escucha alturas logaritmicamente . Esto significa que cuando una frecuencia dada es multiplicada por 2, nosotros lo percibimos como el salto de una octava. Si ud. cambia de La 4 (440 Hz) a su doble (880 Hz), escuchara La 5, exactamente una octava mas arriba:

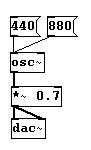
Si desea escuchar una octava sobre 880 Hz, debe duplicarla nuevamente. 880 + 880 = 1760:

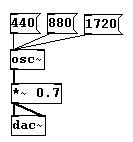
Para ser mas claros: de 30 Hz a 60 Hz, escuchamos una octava, pero de 1030 Hz a 1060 Hz escuchamos un pequeño intervalo. Un salto de 10000 Hz a 20000 Hz es tan solo una octava.

Otro concepto importante: agreguemos un mismo valor a una frecuencia fundamental, de digamos 100 Hz - que es aproximadamente la frecuencia de un cello en la cuerda Sol – a la cual le agregaremos 100 Hz sucesivamente:

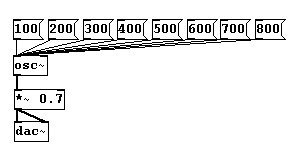
Ud. escuchara una octava de 100 a 200, una quinta desde 200 a 300, una cuarta desde 300 a 400, etc. En matemáticas esto es un proceso de suma en el cual el mismo valor es agregado cada vez. Sin embargo nuestras orejas perciben que esta cantidad es mas pequeña con cada paso:

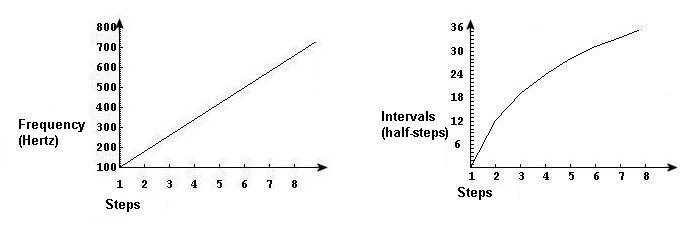
El gráfico de la izquierda muestra la función matemática – una función lineal. El de la derecha muestra lo que escuchamos – una función logarítmica.

Si desea escuchar una progresión lineal , proceso por el cual el mismo intervalo se suma, por ejemplo una octava, la función matemática tiene que ser exponencial:

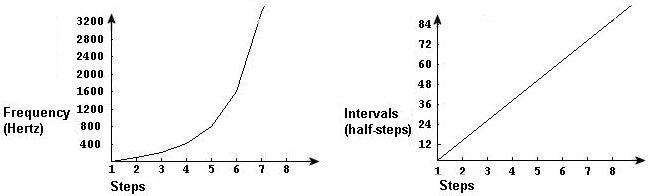
La conversión de progresiones lineales a logarítmicas en Pd se cumple al usar MIDI numbers y frecuencias. Los MIDI numbers reflejan como escuchamos en que los intervalos que escuchamos corresponden a un intervalo equivalente a otro intervalo en MIDI numbers: Un numero entero por cada medio tono. Se pueden convertir valores de frecuencias y MIDI numbers en Pd así:

Una pequeña tabla de MIDI numbers, frecuencias y nombres tradicionales:

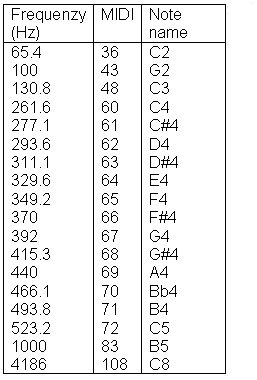
Nota: Los osciladores como “osc~” o “phasor~” deben recibir valores en Hertz.

---

Uno debe recordar que para el Pd, el sonido es solo números. Las posiciones de la membrana del parlante son números entre -1 y 1.

Los objetos como “osc~” generan una muy rápida secuencia de números entre -1 y 1 que se envían al parlante por el objeto “dac~”. Para ser especifico, 44100 números por segundo son generados y enviados. El parlante hace 44100 pequeños movimientos en un segundo. Este numero, 44100, denomina el sample rate (= frecuencia de muestreo).

En Pd, cada sonido se produce usando números entre -1 y 1 a una frecuencia de 44100 números por segundo (sample rate). Cada numero individual es denominado sample.

Todos los objetos de Pd que generan o procesan data a esta velocidad tienen el tilde “~” en su nombre. Estos objetos se conectan con cables gruesos. A esta serie de números la denominamos signals.

Cuando quiera, puede darle una nueva frecuencia al objeto “osc~”. El cable en esta conexión es fino, por que el input no esta en transmisión constante. Aunque el outlet del objeto “osc~” esta constantemente enviando signals, (numeros entre -1 y 1, 44100 veces por segundo = hertz).

No puede conectar un number box al outlet del objeto “osc~” si desea ver los números. Los number boxes solo se usan en conexiones “control” y no conexiones signal. Las conexiones signal son muy rápidas: no puede ver 44100 numeros diferentes en un segundo. Sin embargo puede ver números de una conexión signal con el objeto “snapshot~”. Como input recibe signal y bang, que cuando clickeado muestra el numero signal correspondiente al click. Para ver este numero, puede poner un number box o un objeto “print” a su outlet:

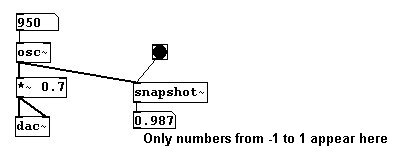
Si desea un muestreo constante, conecte un metrónomo rápido:

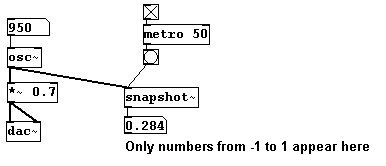
En Pd-extended, tambien puede usar “unsig~”, que tiene incorporado un metrónomo. Ingrese el valor para el metrónomo en su argument:

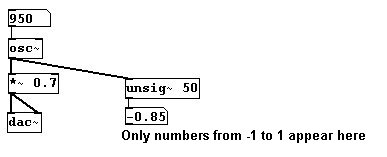
También puede usar “sig~” para convertir un numero control level a signal level. El valor ingresado se emite 441000 veces por segundo.

---

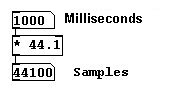
Como con frecuencia (y también amplitud, lo veremos en el próximo capitulo), Hay dos unidades para medir el tiempo en Pd: samples y milisegundos. Generalmente se usan samples para contar signals y milisegundos para control data.

Convirtiendo duración en milisegundos a duración en samples:

---

Valores MIDI son gradualmente desplazados. (una transición desde temperamento igual a afinación aleatoria):

patches/3-1-1-2-1-random-offset.pd

---

a) Cree un glissando que escuchemos como lineal y otro que escuchemos como logaritmico desde do 3 a do 6.

b) Cree una escala de cuartos de tono.

---

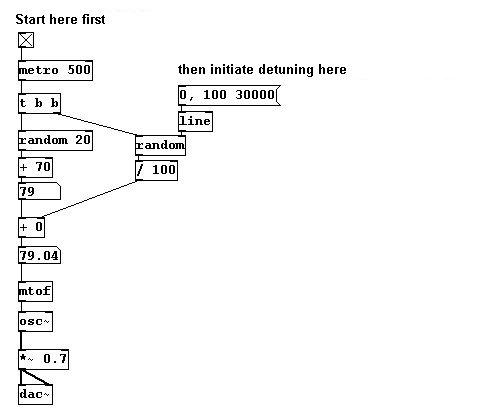El numero 44100 fue elegido por una buena razón. Como mencionamos anteriormente, los humanos escuchamos hasta 20000 Hertz como mucho. En 1928 el físico norteamericano Harry Nyquist (1889-1976) propuso la teoría que establece que una frecuencia de el doble que la frecuencia original es necesaria para (correctamente) representarla digitalmente ("Nyquist-Shannon sampling theorem").Concretamente esto significa que se necesitan los valores máximo y mínimo de cada periodo para representar correctamente la forma básica de una forma de onda; dos puntos por periodo:

Para una onda de 20000 Hz, que tiene 20000 periodos por segundo, necesitamos por lo menos 40000 puntos por segundo para representarla fielmente. Para asegurar que todo el espectro audible para los humanos este incluido, el sample rate de 44100 fue elgido para los Cds de audio. Esto significa que ondas de hasta 22050 Hz pueden ser capturadas. Para las computadoras hay una amplia selección de frecuencias, desde 8000 Hz para sonidos de sistema hasta las grabaciones de alta calidad que funcionan con un sample rate de 48000 Hz (48 kHz kilo = mil), 96 kHz o hasta 192 kHz.

---

Aquí queda claro que el proceso en simultaneo de varias signals es un esfuerzo para la computadora. Imagínese trabajando con 100 objetos “osc~”. Cada uno genera 44100 números por segundo y estos deben estar sincronizados con los demás. Por eso Pd ofrece la posibilidad de apagar el DSP (digital signal processing) en su ventana principal. Esto evitara trabajo innecesario al procesador.

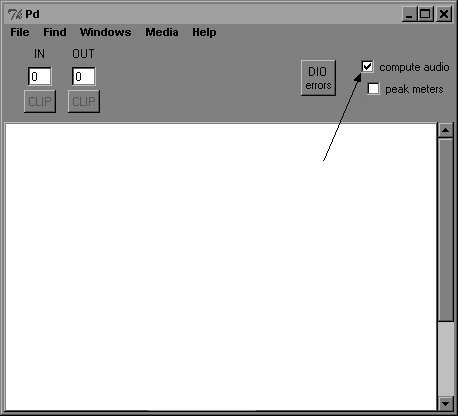
También puede enviar este comando; el receptor “pd” en este caso es el programa mismo:

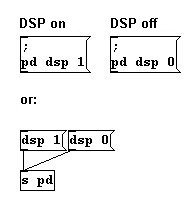
En computer music, cuanto mas rápido es el procesador, mas alta es la performance.

El Pd alivia la carga trabajando con bloques de samples en lugar de uno a uno. Esto mejora mucho la performance. El tamaño de bloque standard es de 64 samples, aunque esto puede ser modificado. Mas sobre esto en 3.8.1.1

---

Previamente se dijo que “dac~” enviá números generados por el Pd a la membrana del parlante (3.1.1.1.1), pero esto esta muy simplificado. Mas precisamente, la placa de sonido en la computadora, convierte los números en una corriente eléctrica con voltaje variable ("digital-analog-conversion" o "da-conversion"); la posición de la membrana es determinada por la cantidad de voltaje. Por el otro lado, las fluctuaciones de la membrana del micrófono se convierten en corriente variable, que luego es digitalizada en la placa de sonido.

---

Las ondas de sonido, en contraste con las olas (ondas en el agua), son longitudinales. Las ondas longitudinales, también llamadas ondas de compresión, se caracterizan por vibrar sobre su dirección de movimiento. (por el otro lado las ondas transversales se caracterizan porque sus oscilaciones ocurren perpendiculares a la dirección de propagación.) Para mayor información consulte textos de física del secundario.

---

El objeto “mtof” convierte MIDI numbers en frecuencias. La formula para este calculo es la siguiente:

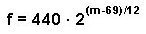
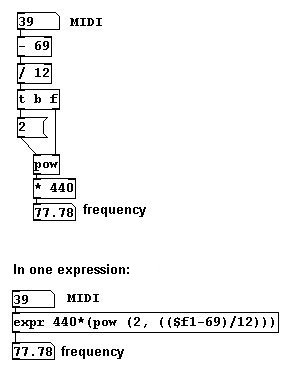
Para calcular la frecuencia de un tono en “temperamento igual” que esta a cierta distancia de una frecuencia dada, use esta formula:

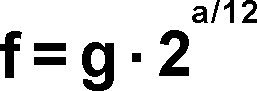`f` es la frecuencia que quiere saber, `g` la frecuencia de un tono dado, `a` el intervalo en medios tonos.

Por ejemplo, si desea calcular la frecuencia de `do 5` y sabe que `la 4` tiene una frecuencia de 440 Hz:

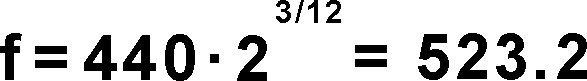En Pd:

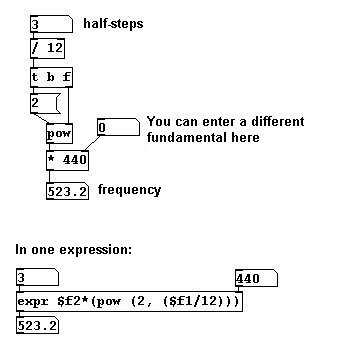
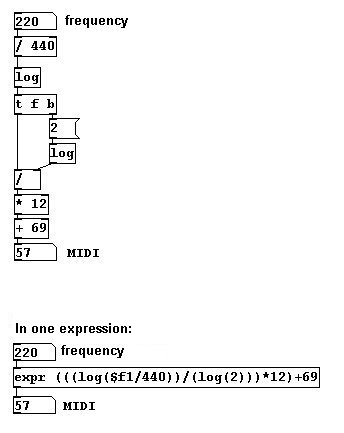
Para la operación inversa – convertir una frecuencia en un MIDI number – la formula es:

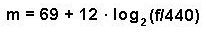
Aunque en Pd solo tenemos el logaritmo natural basado en el número de Euler (la constante matemática `e`); entonces también necesitamos la siguiente formula:

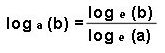
Programado en Pd:

---

Antes mencionamos que los ruidos no son periódicos. Aunque de todos modos Ud. puede imaginar un ruido que dure 10 segundos y luego se repita precisamente como antes. Tal ruido teóricamente tendría una frecuencia periódica de 0.1 Hz. Entonces un ruido seria mas precisamente definido como un sonido aperiodico o con un periodo menor que 20 Hz. Es mas, uno puede decir que las frecuencias del ruido pueden tener un tono fundamental común que es menor a 20 Hz.

Muchos experimentos se hicieron en el campo de la acústica, por ej. el efecto Doppler o los cálculos de longitud de una onda de sonido. Consulte libros de acústica para mas información.

---

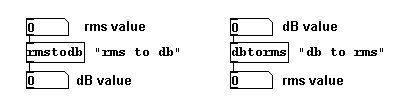
El próximo parámetro de un sonido que veremos es su volumen. Tradicionalmente el volumen en notación musical se establece con las marcas dinámicas como pianissimo, piano, mezzoforte, etc. Su uso es subjetivo y variable dependiendo del instrumento. En física, que es lo que Pd usa como modelo para este parámetro, el volumen es representado con valores objetivos en decibelios o en valores RMS(root mean square = valor cuadrático medio). Ambas unidades son comparables a MIDI numbers y frecuencias (Hz) para alturas. Los decibelios (dB) reflejan lo que escuchamos, donde una `octava` en volumen corresponde a 6 dB. La escala va de 0 a 130 dB – donde un valor de entre 15 y 20 dB es silencio absoluto y todo sobre 120 dB es capaz de causar serios daños al oído. Mas allá de 130 dB percibimos el sonido como dolor. Los valores RMS, como las frecuencias, no corresponden a lo que escuchamos y son valores logarítmicos entre 0 y 1, donde 0 corresponde a 0 dB y 1 a 100 dB. Rms se refiere al promedio geométrico calculado en una serie de valores de amplitud. Estos números son primero elevados al cuadrado, luego se calcula un promedio (sumando todos los valores y dividiéndolos por la cantidad de elementos), y luego la raíz cuadrada de este promedio es calculada. El valor rms en una señal de audio se calcula usando una porción de señal de audio de duración especifica; para una señal muy fluctuante como un tono, le da la idea del valor promedio de amplitud de señal. Estos objetos se usan para convertir entre uno y otro en Pd:

El volumen de una vibración es determinado por su amplitud, lo que es el grado en que la membrana se mueve hacia adelante o hacia atrás con respecto al punto neutral de descanso (la posición 0). Cuanto mayor sea el movimiento de la membrana, mas fuerte sera el volumen percibido. Una representación en un eje se ve así:

No esta suficientemente enfatizado: hasta que esto se envié a los parlantes con la ayuda de el objeto “dac~”, el Pd solo trabaja con numeros. Si un sonido es suave, quiere decir que no usara el rango completo de -1 a 1, sino algo mas cerca del 0 como por ej. -0.5 a 0.5. Esto es posible en un patch multiplicando los números generados por el objeto “osc~” por determinado factor:

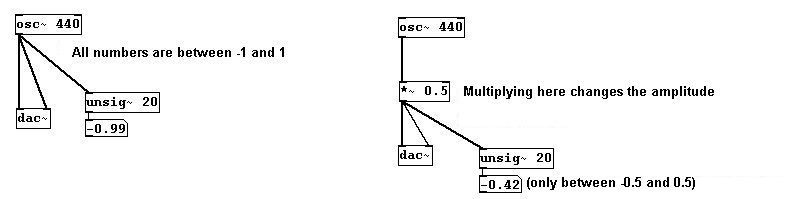
Puede usar este método para controlar el volumen, cualquier nivel desde silencio absoluto hasta el máximo posible (que depende de los parlantes y el amplificador que este usando, claro).

También puede usar un HSlider (Put HSlider) y setear su rango entre 0 y 1 (como en Capitulo 2.2.2.3.2 y 2.2.4.3.4):

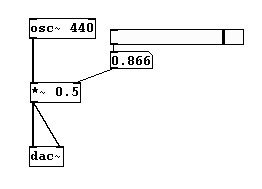
Aunque, mover muy rápido este slider resultara en sonidos disruptivos. Esto es por que signals (calculadas en samples) entran en conflicto con procesos del control level (calculadas en milisegundos). Si es solo para algunos números como previamente con los factores 0, 0.1, 0.4, 0.7, y 1, esto es irrelevante, pero mas alla de cierta velocidad esto tendra un rol significante. Para evitar este problema, debe reemplazar la conexión de control con una de signal. Use el objeto “sig~” para convertir:

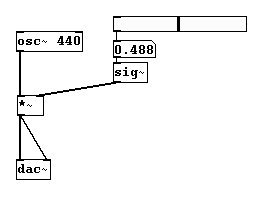
Esto asegura que los números generados por el oscilador (44100 números por segundo) y los generados por la multiplicación (“sig” los convierte exactamente en 44100 por segundo) estén sincronizados. Nota: si una señal signal se conecta al objeto “*~” en su inlet derecho, el objeto no debe tener un argument: si ingresa un argument (por ej. 0.5 como en el ejemplo previo) el objeto recibirá control data en su inlet derecho.

Para crear un crescendo o un decrescendo, debe usar “line~”:

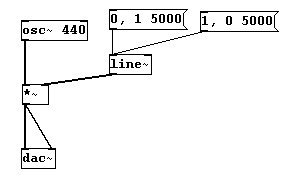
Aquí hay una forma elegante de usar un slider como regulador de volumen (“potenciómetro”):

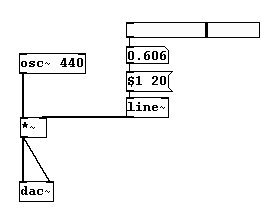
Esto ejecuta un pequeño crescendo/decrescendo entre cada paso. Llenando pasos con valores intermedios de esta forma se denomina “interpolation” (como se vio en alturas en el Capitulo 2.2.3.2.3).

Puede calcular el volumen de un sonido dado usando “env~”, que emite por su outlet el volumen en dB. Siempre debe definir un lapso de tiempo sobre el cual el promedio se calculara; su argument se da en samples (usualmente este numero es una potencia de 2):

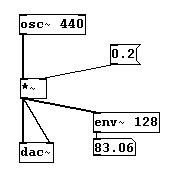
La conversión a rms ...

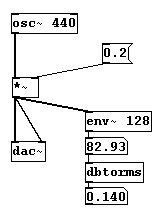
... deja en claro que los factores entre 0 y 1 no deben ser confundidos con valores rms entre 0 y 1.

Como mencionamos anteriormente, la percepción aureal humana del volumen y la altura no corresponden a las medidas de la fisica (como observamos en el par de diagramas para alturas en frecuencias e intervalos). Un simple truco para crear un crescendo/decrescendo mas lineal es usar el cuadrado de sus valores:

Uno puede probar varias posibilidades, aunque, el final, la forma en que el volumen crece o decrece es una decisión compositiva. Lo que constituye una `octava de volumen ` no puede ser objetivado de la misma forma que en `octava de altura`.

En Pd hay un objeto GUI para visualizar la amplitud: el VU meter ( Put VU). Toma un valor en dB por su inlet. Trabaja como una consola de mezcla tradicional: 100 dB se muestran como 0 dB y los desvíos hacia arriba o abajo se muestran en rangos positivos o negativos respectivamente. Debe tener esto en cuenta al conectarlo. Simplemente haga una resta de la salida de “env~”:

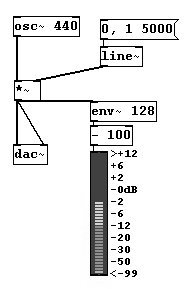
Entonces VU muestra los cambios de volumen gráficamente. (VU es por “volumen”).

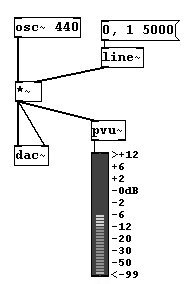
En Pd-extended también puede utilizar el objeto ”pvu~” para la conversión de VU meter:

---

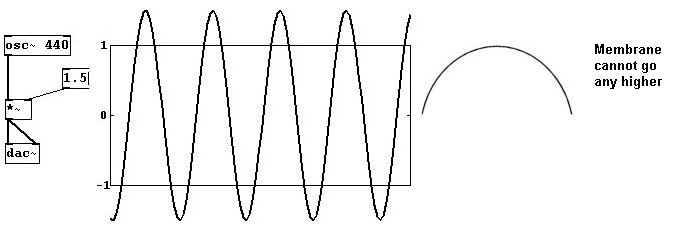
Otra cosa importante: amplitudes mayores a 1 y menores a -1 seran `recortadas`. Si “dac~” enviá a la membrana del parlante un valor fuera del rango -1 a 1, la membrana simplemente se queda en ese extremo.

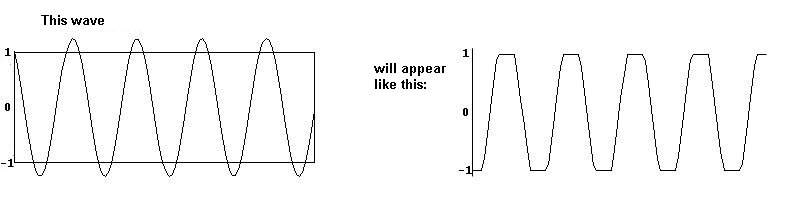
Elevar el volumen de un sonido al punto de “clipear” resulta en un efecto denominado overdrive.

Otro problema ocurre cuando la membrana del parlante tiene que recorrer un intervalo largo de repente (por ej. cuando enciende un sonido); el resultado es un “click”:

Esto es extremadamente notorio cuando el sonido exhibe un movimiento de membrana muy suave, como en un tono sinusoidal. El `salto` se ilustra claramente en el siguiente gráfico:

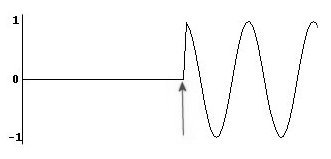
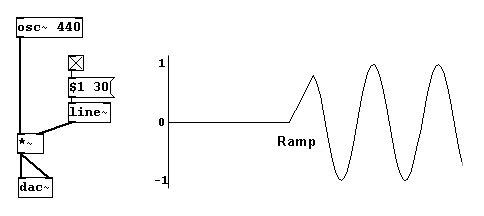
El `salto` es usualmente un movimiento mas rapido que 30 ms. Para evitar este click, debe construir lo que de denomina “ramp”(rampa), un crescendo muy veloz al principio y al final:

---

En Pd también puede ajustar desde que posición de membrana debe comenzar (o debe saltar) una onda de sonido. Esto se denomina Fase de una onda. Puede ajustar la fase en Pd en el inlet derecho de un objeto “osc~” con números entre 0 y 1:

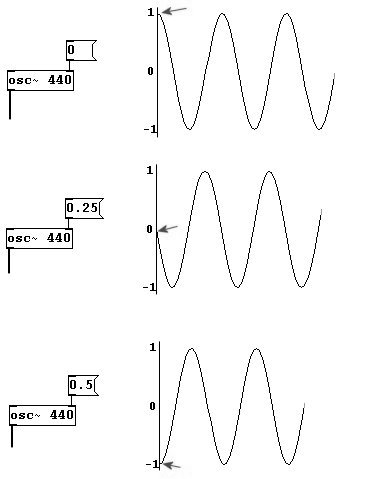
Un periodo entero de la onda esta contenido en un rango de 0 a 1. Aunque a menudo se suele referir a esto en grados, donde un periodo entero tiene 360 grados. Uno dice por ej. “un desplazamiento de fase de 90 grados”. En Pd el valor para ese desplazamiento de fase es de 0.25.

Un desplazamiento de fase no tiene mucho efecto en lo que oímos. Sin embargo regresaremos a este concepto mas adelante.

---

Digamos que ud. tiene estos dos osciladores:

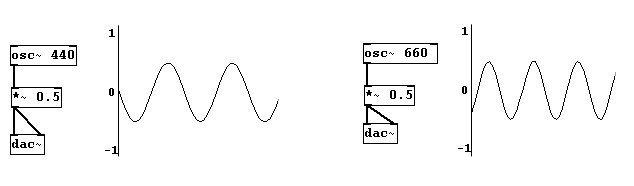
... y los conecta a “dac~”. Resulta esto:

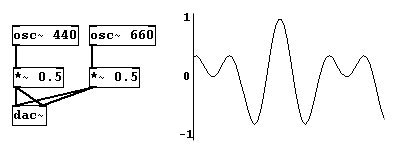
Debido al factor multiplicador, las ondas individuales solo van de -0.5 a 0.5. Aunque juntandolas van de -1 a 1 y tienen una forma mas compleja. Esto es por que las ondas de sonido son aditivas. Simplemente enunciado: todas las vibraciones ocurren en el mismo aire. Su cualidad aditiva también implica cancelaciones. Ondas opuestas, donde una “se mueve hacia atrás” mientras la otra “se mueve hacia adelante” cancela ambas. Esto sucede cuando vibraciones de la misma frecuencia están 180 grados fuera de fase:

Cuando muchas fuentes de sonido están involucradas, debemos multiplicar el sonido total por un factor apropiado para evitar exceder los limites de 1 y -1:

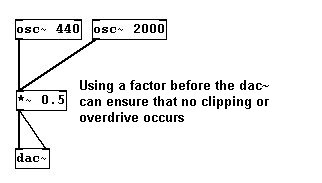
En este caso, ambos osciladores están simplemente conectados a un objeto de multiplicación. Esto las suma automáticamente (cuando varias señales signal se conectan al inlet de un objeto, primero son sumadas y luego procesadas acorde al objeto) antes de de efectuar la multiplicación.

---

Para crear un acorde con volumen variable para cada nota del acorde:

3-1-2-2-1-chord.pd

---

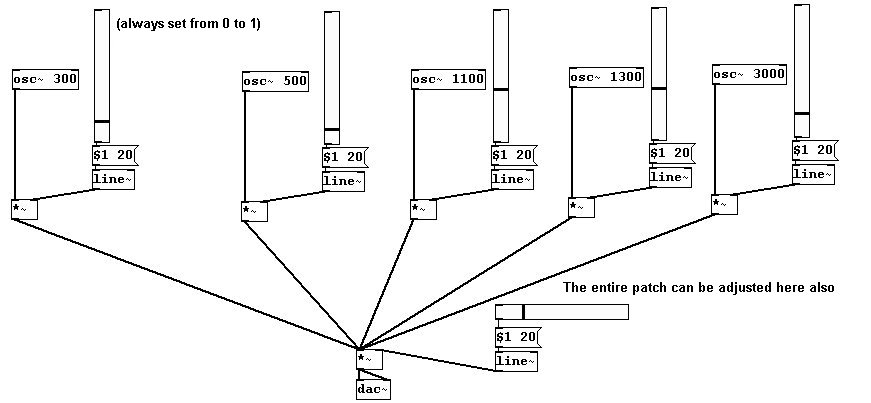
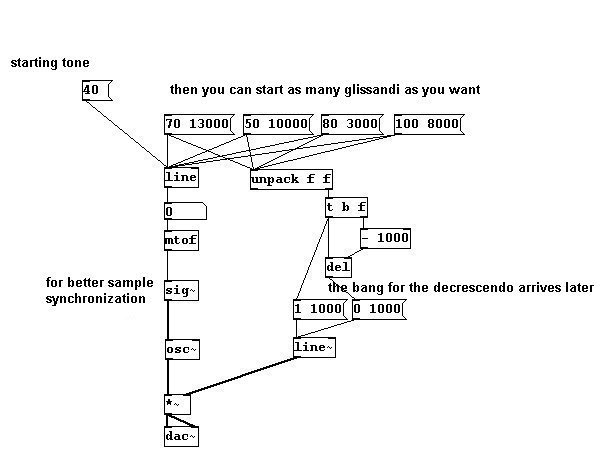
Glissando que crece y decrece suavemente al principio y al final:

patches/3-1-2-2-2-glissandi-dim.pd

---

Diga algo al micrófono y modifique su volumen :

patches/3-1-2-2-3-edit-input.pd

---

Pongámonos “sinfónicos”: por que no usar 20 osciladores a la vez?

patches/3-1-2-2-4-oscillatorconcert1.pd

Primero haga el subpatch "o1":

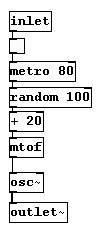
... haga múltiples copias ...

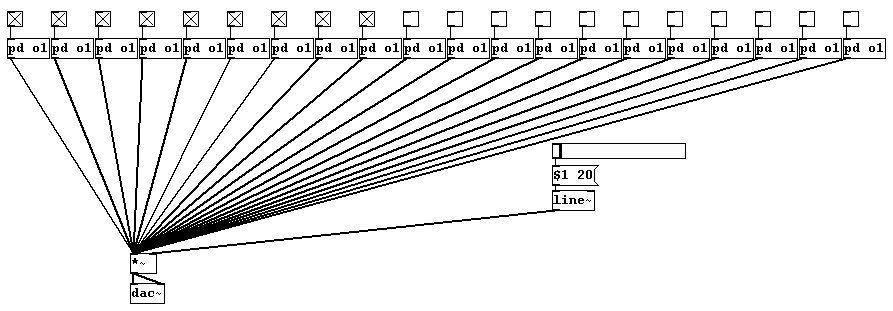
... luego enciéndalos todos!

Por supuesto, los parámetros para cada oscilador se pueden ajustar – ahí hay algo con que jugar:

patches/3-1-2-2-4-oscillatorconcert2.pd

La velocidad del sonido a 20 grados centigrados (68 grados Fahrenheit) es aproximadamente de 343 metros por segundo. Puede calcular el largo de un periodo en el espacio y verificar su resultado inmediatamente...

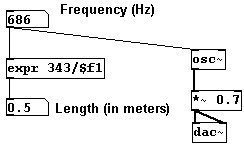
... al mover su cabeza medio metro hacia atrás o hacia adelante mientras escucha una frecuencia de 686 Hz: claramente puede escuchar los picos y valles de la onda. (nota del traductor: pruebe de desconectar un cable de “dac~” para este experimento, puede resultar mas claro.)

---

a) Cree acordes glissando (aleatorios) que tambien tengan cambios de volumen aleatorio en cada nota del acorde.

b) Cree un patch en el cual el volumen en una entrada de micrófono controle la frecuencia de un oscilador (luego use varios, cada uno con un offset diferente)!

---

Muchos de los objetos vistos en el Capitulo 2 también tienen una versión con tilde. Funcionan igual pero con signals en lugar de control data:

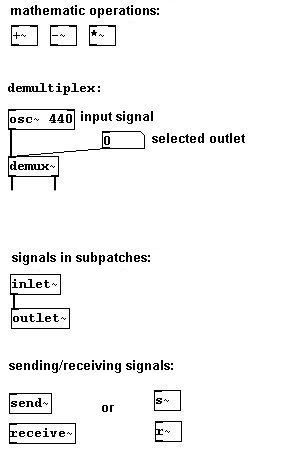
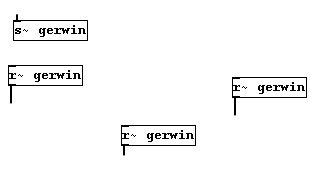
Puede usar “send~” con muchos objetos “receive~”, pero solo un objeto “send~”: (nota del traductor: un solo “send~” por cada argument)

También puede canalizar muchas señales diferentes a un lugar central (por ej. al objeto “dac~”) usando “throw~” y “catch~”:

---

La profundidad de bit es también un concepto importante en Pd. El procesador de la computadora solo trabaja con código binario, ej. 0 y 1. El numero de bits muestra cuantos lugares se usan para ceros y unos. Si tan solo se tienen dos lugares, puede hacer 2², que equivale a 4 combinaciones diferentes:

       0 0
       0 1
       1 1
       1 0
      

Cuantos mas lugares halla, mas detalladamente algo puede ser procesado. Para el Pd, que usa números para calcular frecuencias, amplitudes, etc, esto significa que los números pueden ser procesados mas precisamente, por ej. mas lugares decimales pueden usarse. El Pd funciona normalmente con 16 bit, la calidad de un CD de audio. 16 bit significa 2¹⁶ = 65,536 posibles valores para cada sample.

Nota del traductor: En realidad internamente el Pd siempre trabaja a 32-bit floating point en todas las operaciones de audio. Es el objeto “dac~” quien trunca estos valores de acuerdo con la configuración de la placa de sonido, que generalmente esta en 16 bit o 24 bit.

---

El volumen y, mas importante, los incrementos de volumen son – en terminos objetivos y subjetivos – fuertemente influenciados por factores como: características arquitectónicas del recinto o cuarto, edad de quien escucha, etc. No hay un solo termino preciso de medida de volumen, aunque hay teorías de presión de sonido e intensidad de sonido. Para mas información es altamente recomendado que consulte libros de acústica.

---

Habrá notado que para partes significantes de producción de sonido en Pd dos unidades diferentes se usan: frecuencia y MIDI numbers para altura, rms y decibelio para amplitud y milisegundos y samples para tiempo.

Para el ultimo de estos, el ejemplo en el que se usa “line~” para crear un crescendo/decrescendo que se dio en la sección 3.1.2.1.1. merece ampliar la explicación:

Si hubiese usado un objeto “line” (sin tilde ~) para esto, seguramente hubiese resultado en poppings indeseados o sonidos saturados. Esto hubiese requerido dos unidades diferentes de medición de tiempo combinadas; el problema es que no están sincronizadas. Los diferentes intervalos numéricos no coincidirían, lo que causaría irregularidades en forma de pequeños retrasos o hasta poppings indeseados.

Como vimos en el Capitulo 2.2.3.3.2, “line” genera un valor cada 20 milisegundos. Esto significa que puede no coincidir con los samples. Habiendo un nuevo sample cada 0.02 milisegundos, un valor de “line” puede no coincidir con un sample mas o menos simultaneo, lo que puede llevar a complicaciones. Aunque un objeto “line~” (con tilde ~) genera una señal con 44100 valores por segundo. Estos 44100 valores son generados precisamente al mismo tiempo que cualquier otro objeto con tilde; siempre están sincronizados. La computadora siempre procesa 44100 samples por segundo cualquiera sea su posición en el patch.

---