| 3.3 Síntesis substractiva | ||
|---|---|---|
| Capitulo 3. Audio | |
|
Claude Debussy respondió una vez a la pregunta de como componía diciendo que comenzaba con todas las notas y luego quitaba las que no le gustaban. Pre-vio la idea de filtrar. En contraste con la síntesis aditiva – que usa lo que se considera el átomo del sonido, el tono sinusoidal, como punto de partida – la síntesis substractiva comienza con todo el sonido y luego lo reduce. Es posible producir un sonido entero causando que la membrana del parlante vibre completamente caótica o aleatoriamente, esto produce todas las frecuencias audibles simultáneamente. El objeto en Pd que produce esto es “noise~”:
En términos técnicos, seria mas preciso nombrar a “noise~” como “random~”, por que produce 44100 números aleatorios por segundo. Estos números ocurren dentro del rango -1 a 1, (posición de membrana).
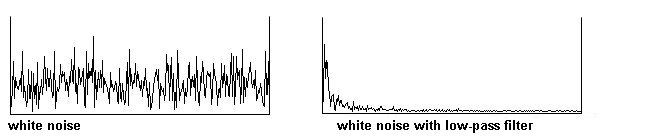
Como la luz, el ruido que contiene todas las frecuencias audibles se denomina “ruido blanco”. La luz blanca normal contiene todas las frecuencias de luz como: luz roja o luz azul que son derivadas de la luz blanca usando filtros.
El Pd tambien tiene filtros como “lowpass”, que solo permite el paso de las frecuencias bajas suprimiendo las altas frecuencias. Esto esta representado en el siguiente gráfico; el eje-x representa la frecuencia y el eje-y su amplitud:
También esta el filtro “highpass”, que solo deja pasar las frecuencias altas:
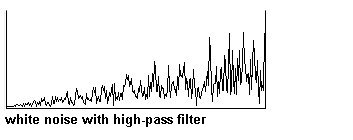
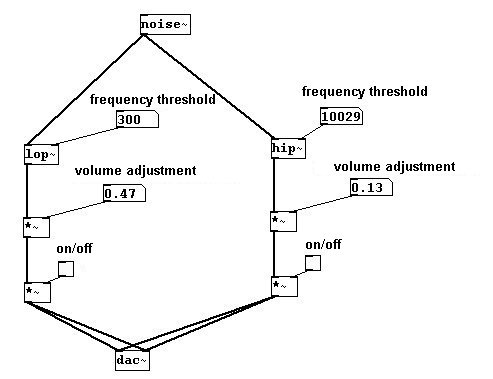
Los objetos del Pd para estos filtros se nombran “hip~” y “lop~”. Su argument o inlet derecho es para la frecuencia desde la cual el sonido sera filtrado.
Como puede notar en los diagramas anteriores, los filtros no son particularmente `marcados`. Puede intensificar su efecto usando uno después de otro (cascade):
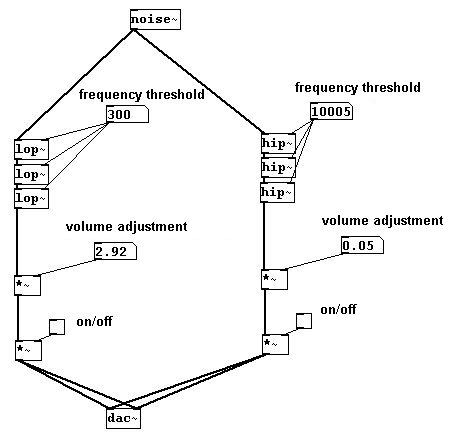
El volumen debe ser reajustado para cada filtro, por que reducen la intensidad del sonido. (Aunque a veces fortalece otras cosas)
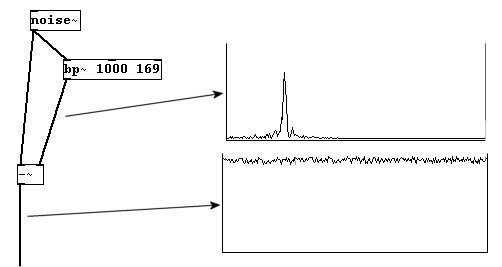
Otro tipo de filtro se denomina “band-pass”. Esto permite pasar solo una pequeña porción de sonido a los lados de una frecuencia central. Como arguments/inlets recibe la frecuencia central y el ancho de banda, denominado “q”.
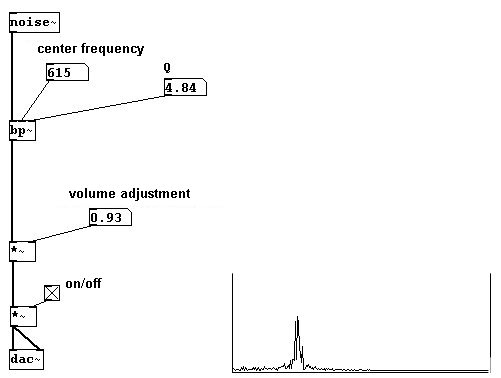
Teóricamente, si el ancho de banda es suficientemente pequeño, se termina escuchando solo un tono sinusoidal:
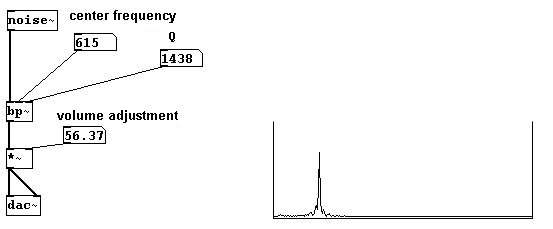
Como claramente puede escuchar, este no es el caso. Un cierto elemento de ruido siempre pasa con un filtro band-pass.
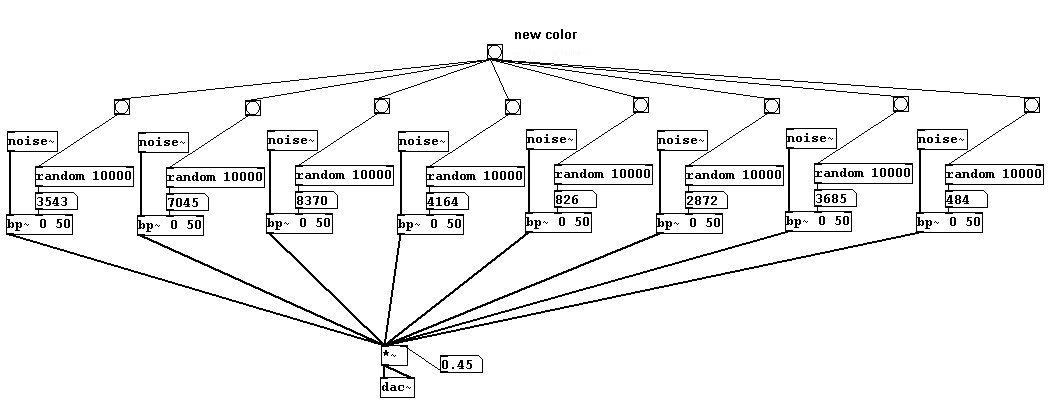
Solo como un ejemplo de como se pueden usar los filtros, aquí hay una distribución aleatoria de filtros pass-band:
patches/3-3-2-1-filtercolors.pd
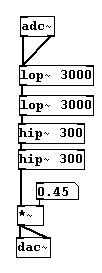
Para transmitir conversaciones telefónicas, se determino que frecuencias de entre 300 a 3000 Hz son suficientes para comprender el habla. Puede simular eso:
patches/3-3-2-2-telephonefilter.pd
El objeto “noise~” causa que la membrana del parlante vibre aleatoriamente. Cuando enciende o apaga este sonido no escucha un click; esto es por que el ruido solo se compone de clicks de variada intensidad. Por esto no necesita un "ramp" (cf. 3.1.2.1.2).
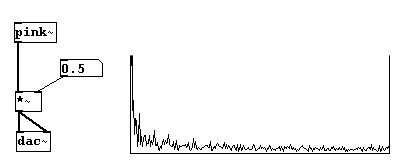
Ademas de el ruido blanco, también existe el “pink noise” = ruido rosa. El oído humano no escucha todas los rangos de frecuencias al mismo volumen. Escucha mejor alrededor de 2000 Hz, es por eso que el ruido blanco suene algo mas “agudo”. Escuchamos considerablemente peor en las frecuencias bajas y altas. Si desea crear un ruido que los humanos perciban con una mejor distribución de las frecuencias, debe adaptarlas a la forma en que escuchamos, ej. las frecuencias bajas deben estar considerablemente mas fuertes que las frecuencias medias. Esta distribución se denomina pink noise y en Pd es generada usando el objeto “pink~”:
Cuando usa un micrófono, la señal a menudo exhibirá una corriente de tierra. Esto se denomina “DC offset”. Resulta como esta forma de onda:
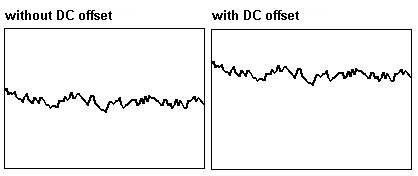
Este desfasaje se debe a una infinitamente lenta vibración cuya frecuencia es cercana a 0. Al ser tan lenta, puede ser filtrada con un filtro high-pass extremadamente grave:
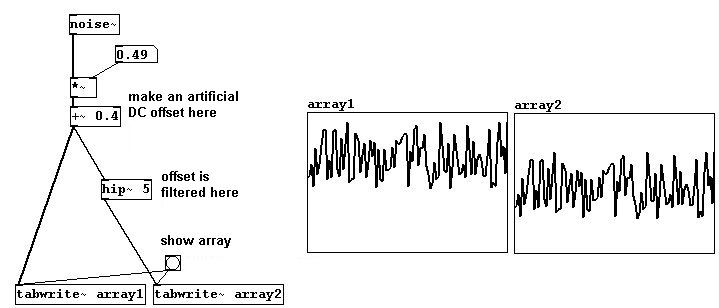
La `vida interna` de un filtro digital es complicada. Aunque uno debe tener una idea precisa de como funcionan: Como describimos en 3.1.1.3.1, el sample rate de 44100 Hz es capaz de representar una onda de como máximo 22050 Hz. Esta onda tendría solo dos puntos por periodo:
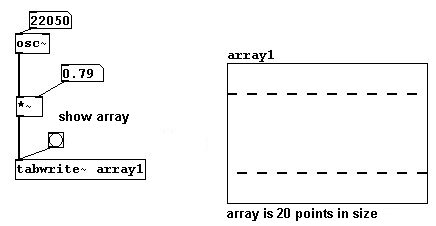
Si ud. mueve esta onda solo una posición, por ej. un sample hacia adelante o hacia atrás, y luego la suma a la onda original el resultado sera que las dos ondas se cancelen una a otra completamente. Este desplazamiento se logra (en pd-extended) con “z~”.
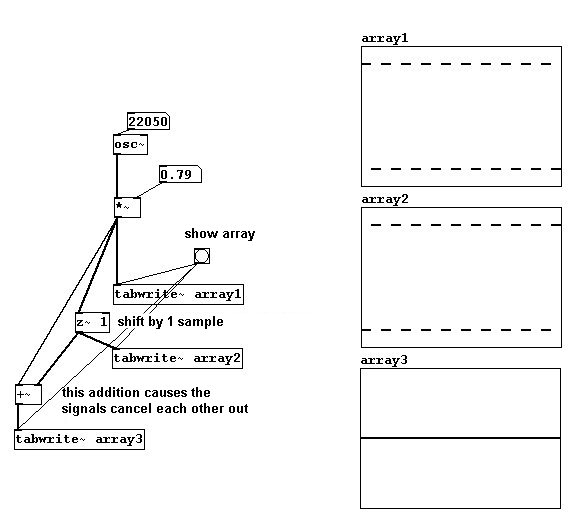
Los filtros digitales emplean este método de retraso de onda de un sample y luego la suman a la onda original para efectuar una cancelación. El objeto “biquad~” puede ser usado para ajustar esto a mano. Ejecuta la siguiente ecuación diferencial: : y(n) = ff1 * w(n) + ff2 * w(n - 1) + ff3 * w(n - 2) con w[n] = x[n] + fb1 * x[n - 1] + fb2 * x[n - 2].
`n` es la posición del sample y ff1, ff2, ff3, fb1, y fb2 son factores definidos libremente. En Pd, el objeto “biquad~” requiere cinco argumentos para ff1, ff2, ff3, fb1, y fb2. Con esta sintaxis: "biquad~" [fb1] [fb2] [ff1] [ff2] [ff3]. Para el caso de de una onda de 22050 Hz como al comienzo de esta sección, puede escribir "biquad~ 0 0 1 1 0". Esto suprime frecuencias altas, especialmente frecuencias de 22050 Hz, que son completamente canceladas. Aquí hay un filtro low-pass usando “biquad~”:
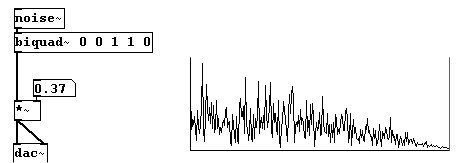
Pude usar la formula de biquad para crear muchos otros tipos de filtros. Por ejemplo, los argumentos 1.41407 -0.9998 1 -1.41421 1 hara un “filtro de rechazo de banda”. Esto es el inverso de un filtro band-pass; rechaza una cierta banda de frecuencias alrededor de una frecuencia central, en este caso 5512.5 Hz. La explicación para este tipo de cálculos llenaría un libro entero. En Pd-extended hay objetos ("band-pass", "equalizer", "highpass", "highshelf", "hlshelf", "lowpass", "lowshelf", "notch") que hacen estos calculos. La ventaja del filtro bicuad es que se logran filtros considerablemente mas marcados que con "lop~", "hip~", o "bp~". La contra es que no solo suprime ciertas frecuencias sino que también intensifica otras al punto de “explocion” (puede verse en la formula que el filtro funciona de forma recursiva).
Con el procesamiento de bicuad tambien puede ver que los filtros emplean desplasamientos de fase. Por eso por ej. un objeto “bp~” no es simplemente la invercion de un filtro de rechazo de banda: