| 3.2 Síntesis aditiva | ||
|---|---|---|
| Capitulo 3. Audio | |
|
La serie de sumas de frecuencias (la serie que resulta simplemente al sumar el mismo valor en Hertz repetidamente), que resulta en una serie de intervalos que decrecen, se denomina serie armónica:
También se puede derivar esta serie repitiendo un experimento hecho por Pitágoras (aproximadamente 582 - 507 a. C.) donde una cuerda es dividida en varias proporciones:

Las razones describen las dos longitudes de la cuerda en relación una con otra.
Cuando una cuerda es tocada con el arco, no solo vibra como un todo, sino que también lo hace en cada proporción de números enteros:
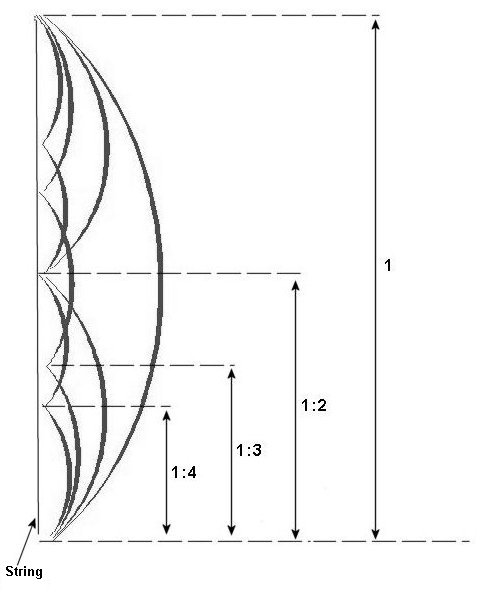
Aquí las razones describen la longitud de la sección vibrante en relación a la longitud entera de la cuerda.
Todos estas vibraciones parciales (llamados `parciales` o `armónicos`) también resultan en el sonido, entonces cada sonido en una cuerda es, de hecho, un acorde!
Algo especial en este acorde es que todas las alturas se juntan y sus volúmenes relativos decrecen a medida que suben las alturas. Cada sonido natural tiene `sobretonos`. Debido a las características del oído, escuchamos todos estos tonos como un solo tono.
En contraste, los parciales superiores (aquellos por encima de la fundamental) no tienen sobretonos. No existe en la naturaleza un sonido aislado sin sus sobretonos, aunque esto se logra electronicamente. Estas se llaman ondas sinusoidales, el nombre deriva de su forma de onda:
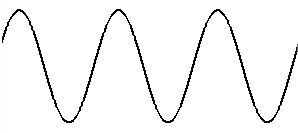
El matemático y físico francés Jean Baptiste Joseph Fourier (1768-1830) descubrió que cada sonido periódico puede ser representado usando solamente ondas sinusoidales (de diferente frecuencia, amplitud y fase), la suma de estas es luego idéntica a la original. Este análisis y su correspondiente proceso matemático es denominado análisis de Fourier y transformación de Fourier.
Usando este principio, es posible crear cada sonido periódico usando varias capas de tonos sinusoidales, este proceso se denomina “síntesis aditiva”.
En Pd, como ya mencionamos, “osc~” es usado para generar ondas sinusoidales. Las ondas sinusoidales son muy características en la música electrónica ya que solo se pueden producir electronicamente.
Usando varios objetos “osc~”, cuyas frecuencias formen una serie aditiva, puede crear un acorde basado en la serie de sobtretonos:
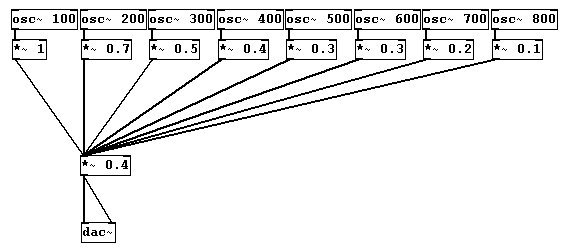
Típicamente, las amplitudes se hacen menores cuanto mayores sean las frecuencias para que el acorde se mezcle mejor (aunque para algunos instrumentos, es característico que determinados parciales suenen mas fuerte que otros a cada lado de ellos, por ej. el clarinete). Su configuración y los relativos volúmenes de sobretonos determinan el color de un sonido. También denominado espectro.
El hecho de que nuestras orejas mezclen los sobretonos se hace mas evidente si cambia la frecuencia fundamental:
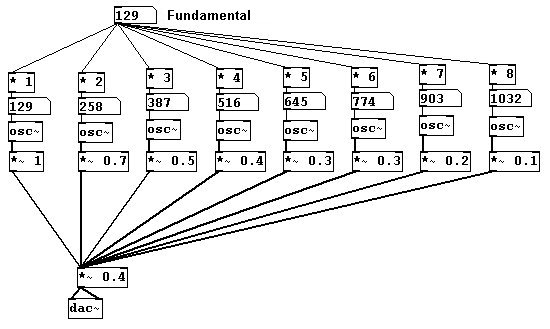
Solo usaremos los primeros ocho parciales aquí. (nota: El termino `parcial` incluye la fundamental pero el termino `sobretono` no. En otras palabras el 1er parcial = frecuencia fundamental, el 2do parcial = el 1er sobretono, 3er parcial = 2do sobretono, etc.).
Aunque quite los parciales mas graves, escuchara la frecuencia fundamental como fundamental cuando la cambie:
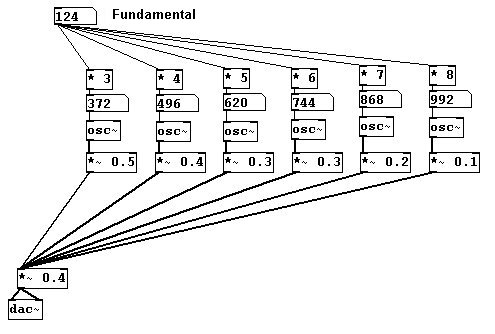
Nuestro cerebro calcula la fundamental basándose en el espectro que queda. Este tono inexistente se denomina tono residual.
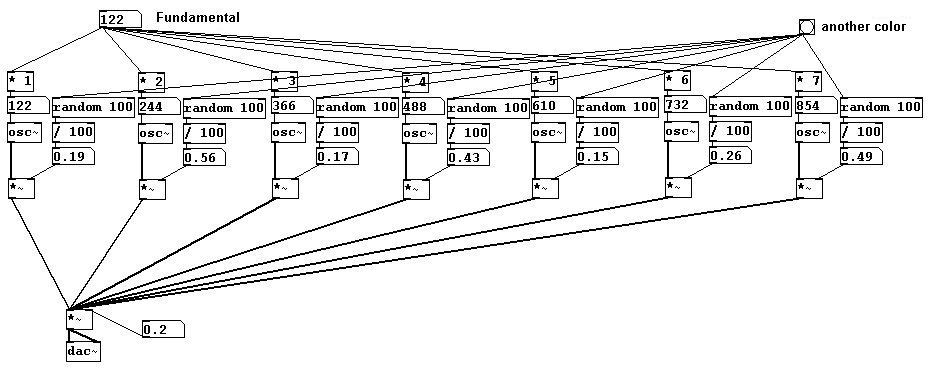
patches/3-2-2-1-random-color.pd
Para economizar espacio, este ejemplo fue limitado a los primeros siete parciales:
Veamos la diferencia entre intervalos naturales y de temperamento igual (primero ingrese la frecuencia fundamental):
patches/3-2-2-3-natural-tempered.pd
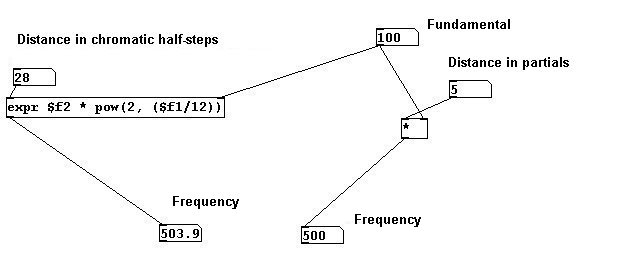
Mostrando la diferencia entre afinaciones naturales y de temperamento igual en cents (milesima de medio tono):
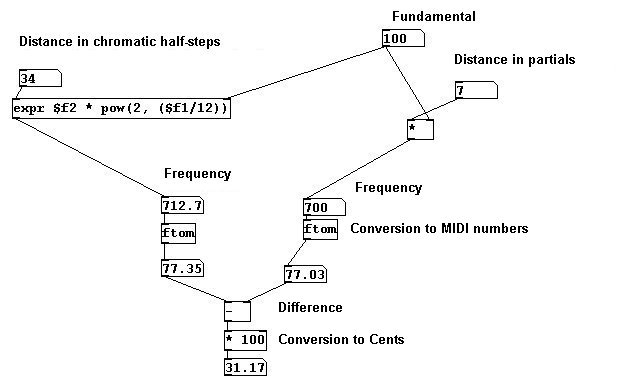
Aquí se muestra que el 7mo parcial es 31 cents mas bajo que el 7mo de temperamento igual.
Una de las piezas pioneras en musica electronica es 'Studie II' de Karlheinz Stockhausen, compuesta en 1954. Este trabajo solo usa tonos sinusoidales y sus mezclas en intervalos no temperados. El autor recomienda que analice esta pieza.