| 3.8 Análisis de Fourier | ||
|---|---|---|
| Capitulo 3. Audio | |
|
Volvamos al concepto básico de síntesis aditiva: un sonido contiene parciales. Si desea saber cuales son las partes componentes de un sonido, puede usar varios filtros pasa banda para cada parcial:
patches/3-8-1-1-analyze-partials.pd
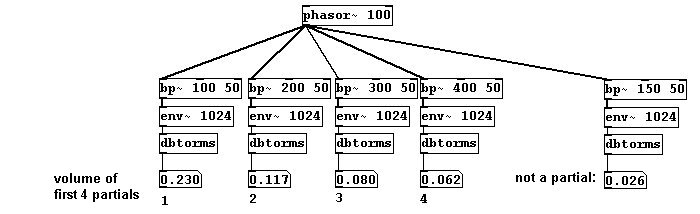
Este proceso lleva a cabo lo que se denomina transformación de Fourier. Divide todo el espectro de frecuencias en partes de igual tamaño y determina la amplitud y la fase de cada parte. Entonces uno puede reconstruir la señal original desde estos valores. La derivación de las partes componentes se denomina análisis; la reconstrucción de denomina resintesis; Puede realizar esto usando “rfft~” e “irfft~”:
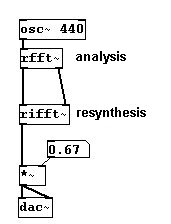
El tamaño de las secciones individuales, denominado “bins”, esta dado por el tamaño del “block”. Como vimos en el Capitulo 3.1.1.3.2, el Pd siempre procesa las tareas por bloque. Normalmente el block size en Pd es 64 samples. Usando “print~” se muestran todos los valores de un bloque dado:

Como con “snapshot~” o “unsig~”, puede ver la amplitud de los valores producidos. Con “print~” puede ver todos los valores generados, limitados en numero a un DSP block. Primero quedémonos con 64 samples; todo el espectro hasta 44100 Hz es dividido en “bins” con un tamaño de 44100/64 = 689 Hz. Lo proximo que tenemos que considerar es que los datos de amplitud y fase en “FFT” no son representados en el valor acostumbrado, sino como valores seno y coseno. Por el momento no profundicemos en este detalle; puede transformar estos datos de forma mas comprensible de la siguiente forma:

Como puede ver, “print~” genera 64 valores de amplitud. La amplitud se da aquí como magnitud, siempre un valor positivo (por que fue elevado al cuadrado). Miremos mas de cerca: excepto por el tercer bin, que tiene un valor de aprox. 32, solo tenemos valores pequeños. No hay cálculos para los números por encima de la frecuencia de Niquist.
Usualmente un proceso de normalizacion se efectuá luego de un proceso FFT, por que los valores son un poco elevados. Primero, este es el tamaño de bloque:
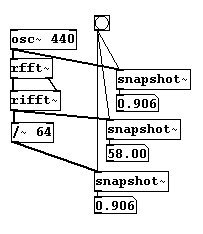
Puede presentar un análisis FFT en un array:
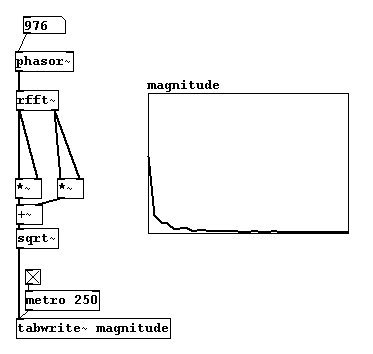
De este modo puede ver el espectro de una señal. Nota: El FFT vuelve la información que ocurre en el tiempo en información de frecuencias; estas se actualizan en cada nuevo block. Denominamos time domain y frequency domain.
En Pd, el block size solo puede cambiarse en un subpatch. Esto se logra usando “block~” :

Cuando elija el block size, considere que bloques mas grandes le permitirá trabajar con frecuencias bajas. Por ejemplo: con un tamaño de 1024 samples, cada bin es 44100/1024 = 43 Hz de tamaño, asi tiene una resolución mas fina. La desventaja es que el proceso demora mas tiempo.
Quedémonos con el block size de 64, que usaremos para analizar el espectro de una frecuencia de 689 Hz. Pero que si otras frecuencias ocurren entre tanto?
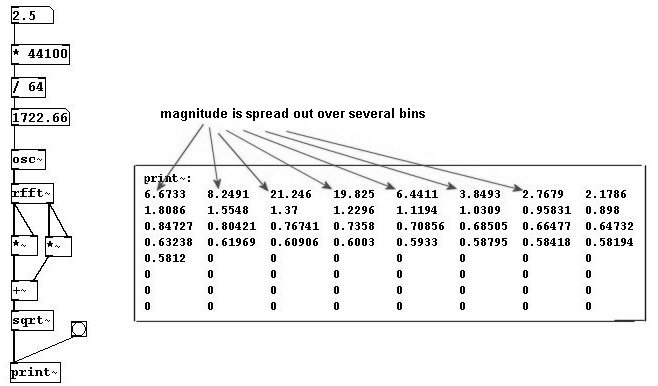
La información esta dividida en varios bins y la fase cambia a cada análisis. Este problema no puede ser resuelto completamente; se debe trucar un poco. La forma normal de resolver este problema es usar windows superpuestos como en síntesis granular; debe crear una una versión `windowed` del original. Para esto puede usar “tabreceive~”, un objeto que siempre lee un array dado en block size con una ventana Hanning – aquí de 64 samples.
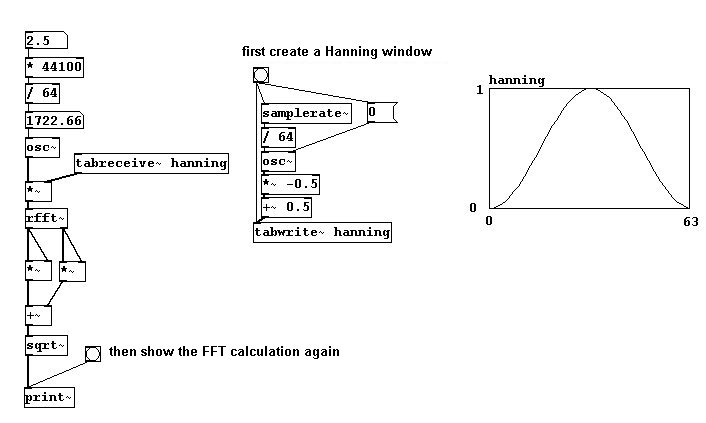
De este modo, los valores de las magnitudes no están `tan dispersos`.

Mas sobre windowing, las windows deben superponerse unas a otras. Esto es realmente fácil en Pd: simplemente ingrese el numero de windows (comúnmente 4) como segundo argument de “block~”. El resultado al final tambien debe ser windowed. La normalizacion apropiada para 4 ventanas superpuestas es de (3 * block size) / 2. Como esta usando “block~”, todo esto debe hacerce en un subpatch.
patches/3-8-1-2-fft-subpatch.pd
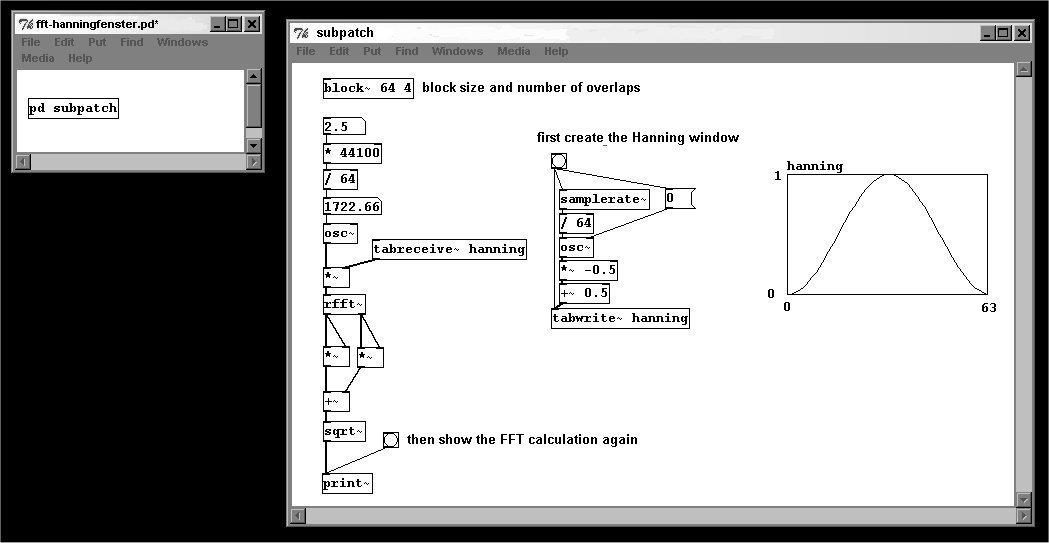
Al superponer y windowizar, hay buenas chances para que la señal sea correctamente analizada.
Por supuesto, lo que es util de FFT, es que los valores que determina pueden ser modificados antes de resintetizar los componentes en un resultado sonoro. Por ejemplo, puede llevar ciertos bins a mayor o menor volumen; Puede hacer filtros como high-pass, low-pass, etc., o `dibujar` uno ud. mismo.
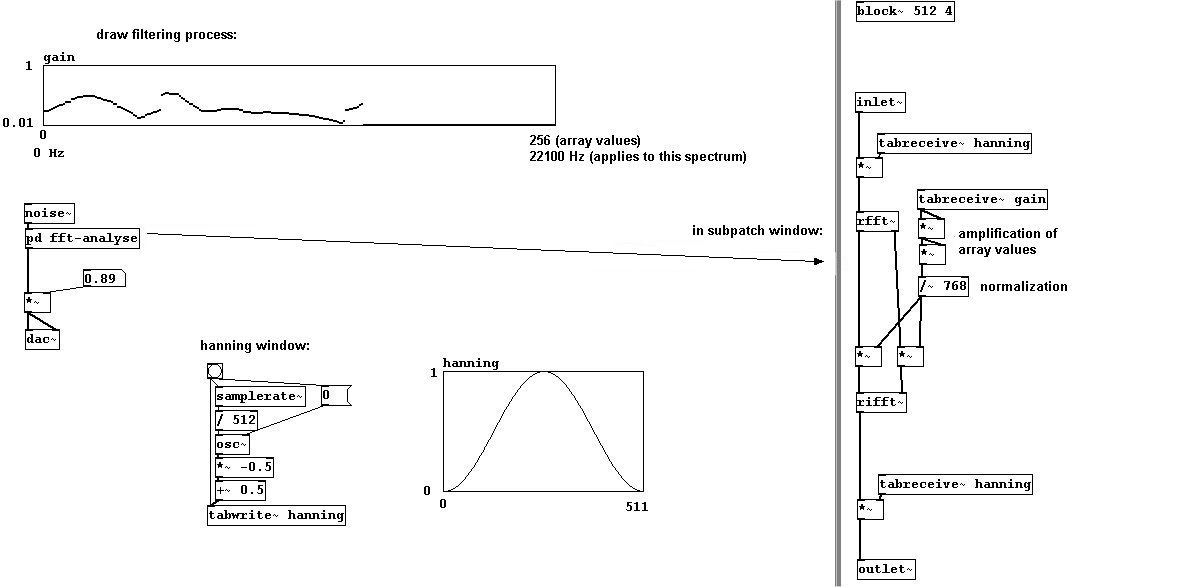
La convulsión es un efecto muy celebrado – plegar una señal con otra; reproducir el promedio de sus amplitudes. El calculo hanning ya debe ser familiar para ud. a estas alturas. Un block size de 1024 samples y cuatro superposiciones es el standard.
patches/3-8-2-2-convolution.pd
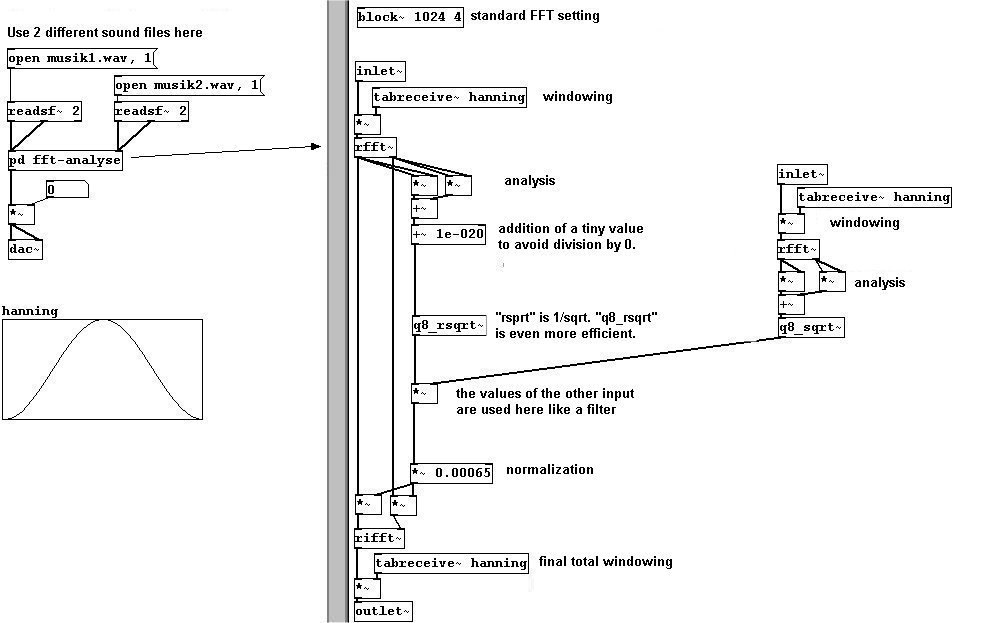
También puede construir un compresor. Esto significa que los volúmenes mas débiles serán amplificados un poco para acercarlos a los volúmenes altos. Simplemente use los valores de magnitud como factores para las salidas de “rfft~”, aunque tenga cuidado que los valores que excedan cierto umbral (“squelch”) serán simplemente cortadas en ese punto:
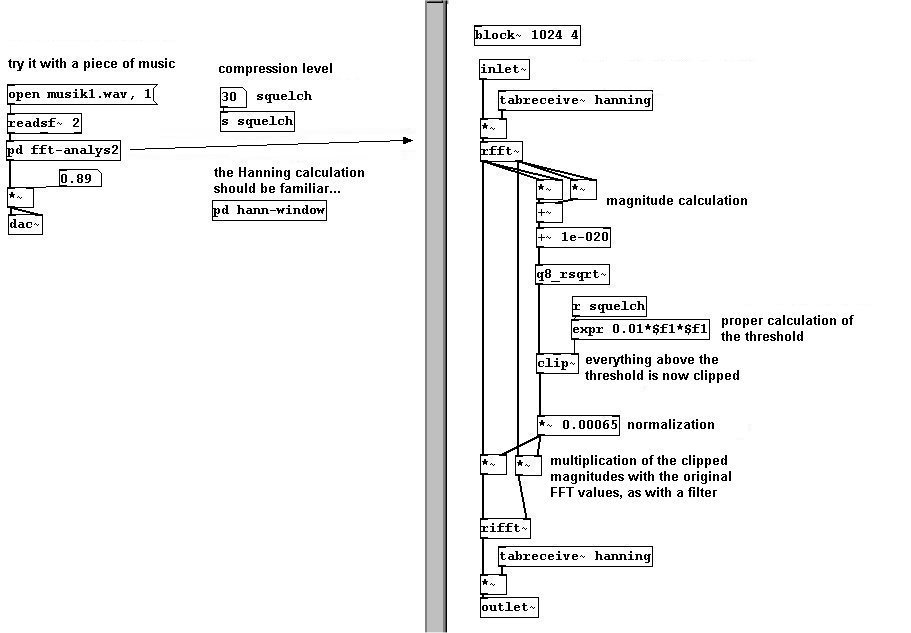
Si implementa esto en el pliego de uno de los dos análisis, tendrá un efecto de convulsión mas rico:
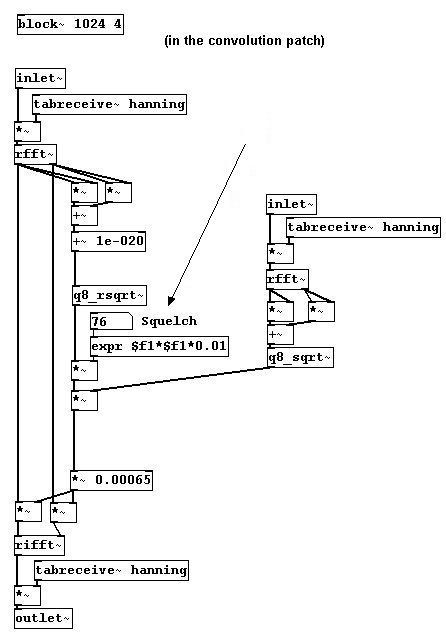
También puede reproducir determinados bins con diferentes cantidades de delay para lograr lo que se denomina “spectral delay”. El análisis FFT se escribe en dos buffers diferentes. Usando un array, determina el delay para cada bin. El máximo tiempo de delay es aprox. 2500 milisegundos, por que tiene un buffer de 10000 milisegundos pero 4 superposiciones (“block~”), lo que significa 10000/4 = 2500. Para ser precisos, en realidad son 2496 milisegundos: 2496 * 44.1 = aprox. 110080 samples, que es 110080 / 512 = 215 posiciones de bin. Desde que la señal de entrada usualmente no cabe en el tamaño de un bin, los valores de análisis están divididos entre varios bins vecinos (cf. 3.8.1.2). Si estos bins vecinos ocurren a diferentes tiempos, puede haber reducciones de volumen.
patches/3-8-2-4-spectral-delay.pd
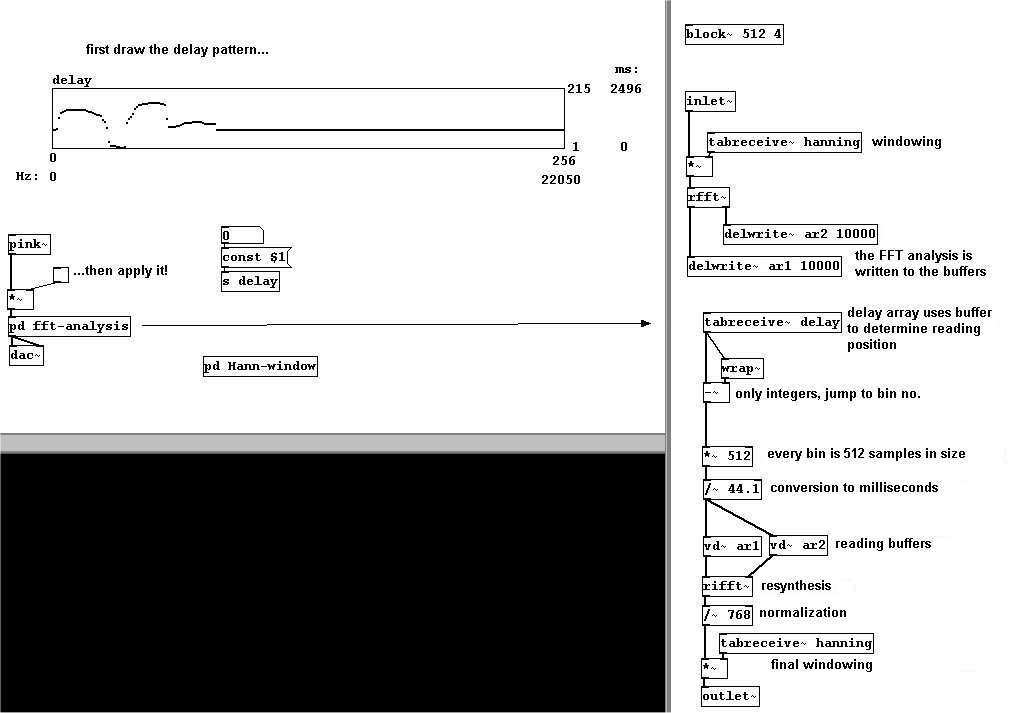
Pruebe esto con una obra musical particularmente llena de eventos!
Hay un objeto en Pd que esta basado en el algoritmo FFT que efectuá el análisis de ambos volumen y frecuencia. Se llama “fiddle~”. También determina los volúmenes de los parciales de la señal de entrada.
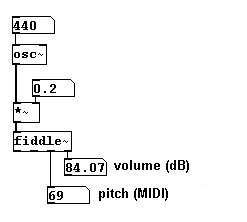
Los argumentos que recibe son: 1. Window size (en samples), 2. Numero de tonos que serán reconocidos simultáneamente (max. Tres tonos diferentes), 3. Numero de picos que encontrar, y 4. Números de picos que saldrán. El estado por default es: 1. 1024, 2. 1, 3. 20, 4. 0. Como outlets (de iz. a der.):1. Altura en MIDI (solo cuando hay un cambio), 2. Volumen en dB (solo cuando hay un cambio extremo (“attack”)), 3. Altura y volumen de la fundamental (en forma de list), 4. Volumen total, y 5. Parciales individuales con sus respectivos volúmenes (en Hertz / rms! - también en forma de list).
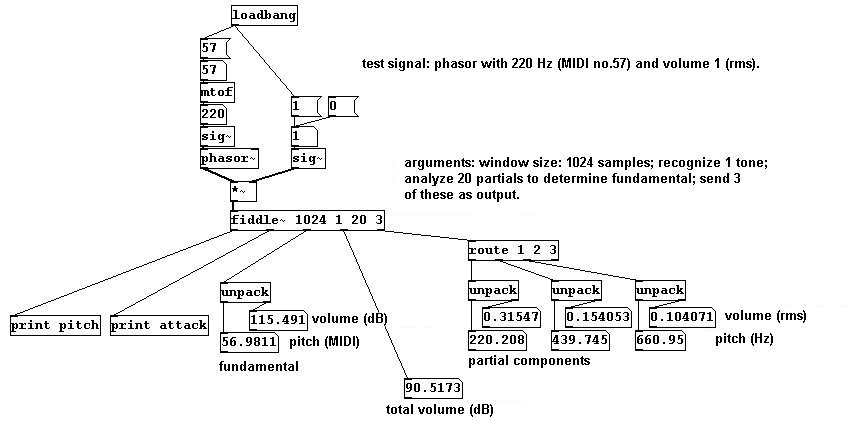
Los messages para “fiddle~”: para evitar un constante procesamiento de data, puede apagar “auto mode” y activar “poll mode” en su lugar; este solo entrega números cuando recibe un bang:
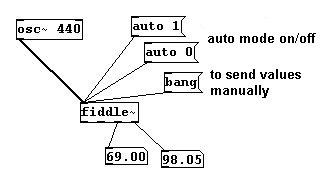
Puede determinar el tamaño del window (múltiplos de dos):
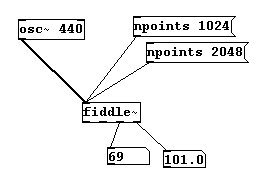
Los parciales superiores no son analizados tan intensivamente como para determinar la fundamental. Puede cambiar esto instruyendo al objeto que analice determinado parcial al menos la mitad de intensivo que la fundamental:
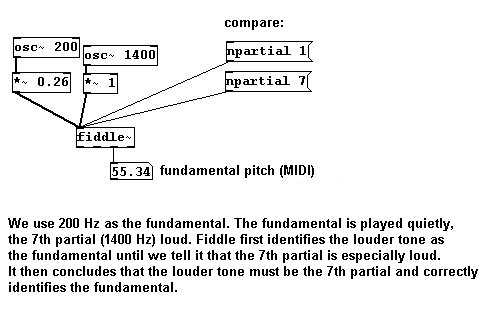
Esto es útil si sabe que determinados parciales en la señal de entrada son especialmente marcados (ej., el tercer parcial de un clarinete).
Nota: La señal de entrada es analizada cada mitad de window size, ej., si el window size es de 1024, entonces 512 samples, lo que es igual a 11.6 milisegundos. La frecuencia mas baja que “fiddle~” puede reconocer es (44100 / window size) * 2.5; para un window de 1024 samples esto es aprox. 108 Hertz.
Aquí hay una forma de construir un afinador:
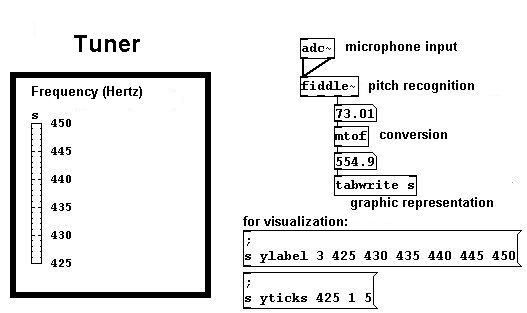
Para la visualización, un array con solo un lugar fue usado.
Para el doblador de octavas descripto en 3.4.2.9, ahora puede usar un micrófono mientras que la fundamental pueda ser usada para los cálculos (mientras la señal sea periódica y pueda ser entendida por “fiddle~”):
patches/3-8-3-3-oktavedoubler-fiddle.pd
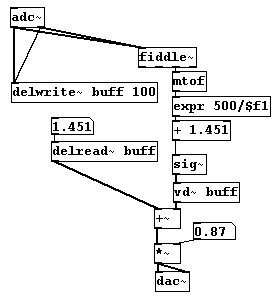
Muchas aplicaciones interesantes pueden ser imaginadas para usar el objeto “fiddle~” de este modo. Un ejemplo prototipico seria una señal de micrófono, como una voz cantante, y `trazar` los contornos melódicos de la voz como un puntero laser:
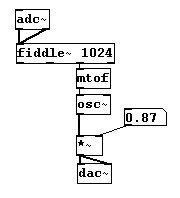
Aquí aparece el siguiente dilema: siempre hay un delay cuando se usa “fiddle~”. Cuanto mas pequeño es el window size, mas corto este sera. Aunque, cuanto mas pequeño sea el window size, mas alto sera el rango de alturas grabes que se podrán reconocer. Ademas, el resultado de “fiddle~” siempre es un poco caótico. Puede minimizar esto viendo 4.3.1.3.