| 3.5 Wave shaping | ||
|---|---|---|
| Capitulo 3. Audio | |
|
En 3.1.1.1.2 aprendió las diferentes formas de onda (sinusoidal, serrucho, triangulo, cuadrada, y pulso). El Pd tiene objetos para dos de estas, “osc~” para las sinusoidales y “phasor~” para las serrucho. Puede usar un array para visualizar las formas de onda:
patches/3-5-1-1-waveform-graph.pd
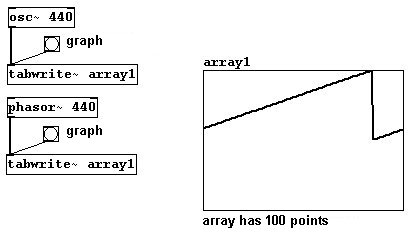
Nota: El serrucho de un objeto “phasor~” siempre va de 0 a 1; nunca va al rango negativo. Sin embargo puede remarcarla haciendo un pequeño calculo:
patches/3-5-1-1-strong-phasor.pd
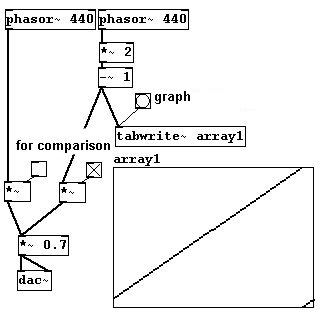
También puede crear otras formas de onda agregando pocas operaciones a “phasor~”. Para esto, necesitara un nuevo objeto: “clip~”, que corta todo fuera de del rango indicado. Como arguments, ingrese dos numeros, uno para el limite inferior y otra para el superior. Los números fuera de estos limites serán cortados.
patches/3-5-1-1-other-waveforms.pd
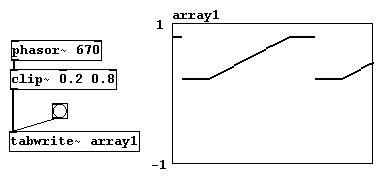
Para una onda triangular:
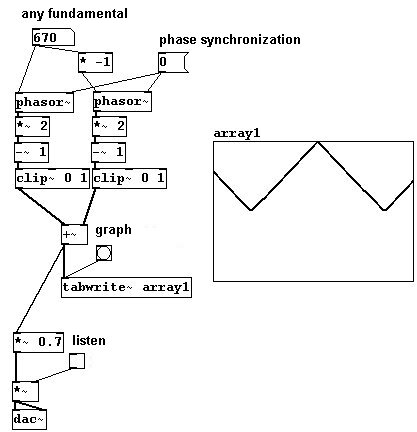
Onda cuadrada:

Pulso:
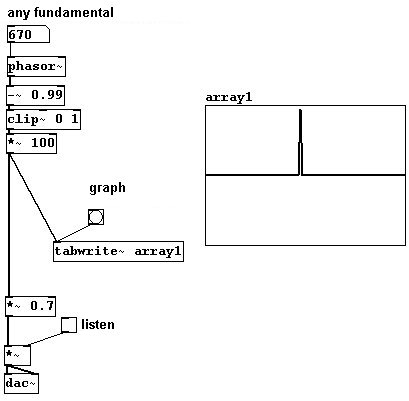
Estas son todas formas de onda standard que exhiben determinadas caracteristicas:
Sinusoidal: un único tono, sin sobretonos
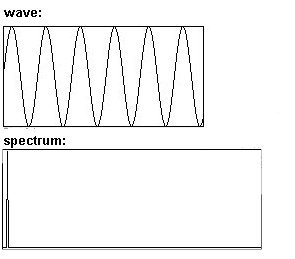
Triangulo: como sinusoidal, excepto que también tiene parciales impar.
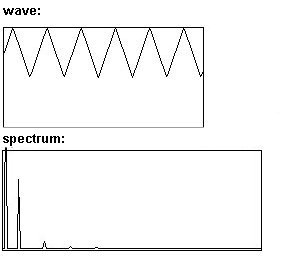
Cuadrada: solo parciales impar
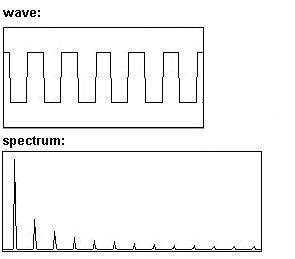
Serrucho: todos los parciales
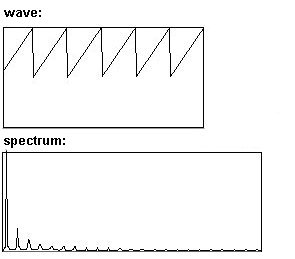
Pulso: todos los parciales presentes en intensidades casi iguales
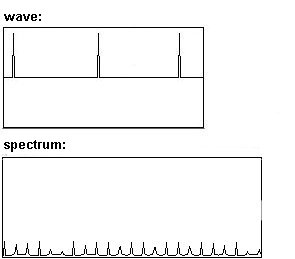
Puede observar que las formas de onda simétricas solo exhiben parciales impar (dentro de cada periodo, caben exactamente dos periodos de cada subsecuente parcial impar; a eso se refiere por simétrico), mientras que las formas de onda asimétricas, ademas, siempre exhiben los parciales par.
Se puede hacer una aproximación a estas formas de onda usando síntesis aditiva:
patches/3-5-1-1-waveform-fourier.pd
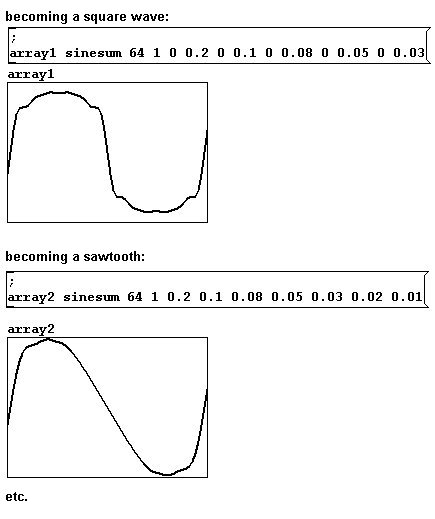
Aquí hay espacio ilimitado para la experimentación y esa es una forma de llegar a nuevos sonidos. También puede dibujar directamente su propia forma de onda en un array. Para hacerlo, debe estar en execute mode y debe mover el mouse hacia una linea del array. El cursor cambiara su dirección:

Mientras mantiene apretado el botón del mouse, mueva el mouse para dibujar su forma de onda.
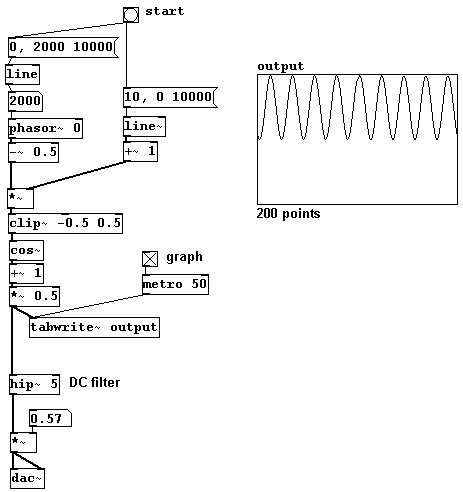
Aunque esto es de alguna forma `tedioso` y `poco elegante`. Examinemos entonces la teoría del `wave shaping`:
Una función lineal conlleva lo que se denomina una “función de transferencia”. Para funciones lineales puede usar “phasor~”, que siempre va de 0 a 1. Puede hacer una onda coseno, por ejemplo, usando el objeto “cos~”, que calcula una función coseno:
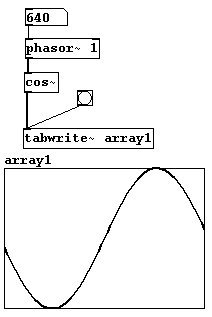
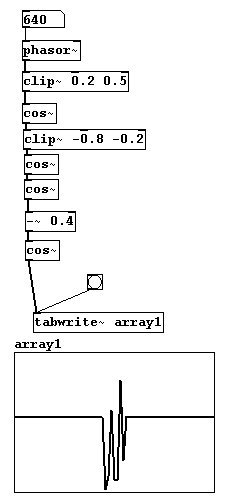
Puede hacer todo tipo de transferencias de este modo; aquí hay otro ejemplo:
patches/3-5-1-2-transferfunction.pd
También puede grabar ruido en un array y luego leerlo periódicamente, es decir, leer lo mismo una y otra vez (cf. Karplus-Strong). Si hace esto mas de 20 veces por segundo, escuchara un tono:

El espectro de este sonido naturalmente es impredecible. Cada vez que llene el array con números al azar del objeto “noise~”, tendrá una nueva onda con nuevas características.
Pero todavía hay mas por hacer. Por ejemplo puede interpolar todos los clicks (saltos largos en la forma de onda) para conseguir una forma de onda resultante mas `suave`. Generemos puntos al azar usando interpolación lineal (“uzi” (Pd-extended) genera un numero de bangs especificado en su argument y los emite lo mas rápido posible):
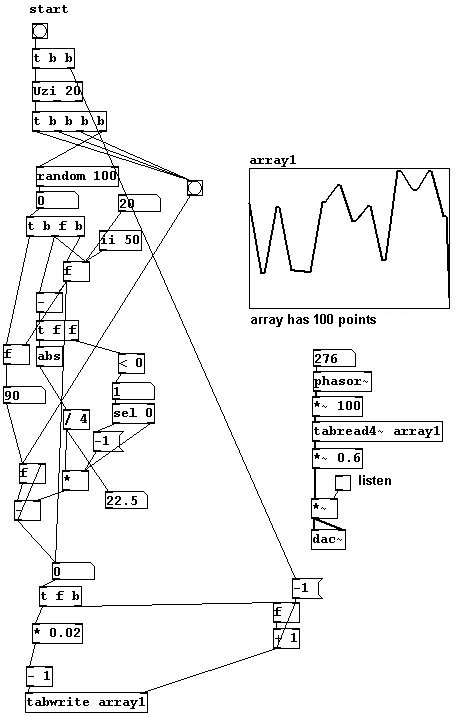
En este ejemplo, siempre se usan cuatro puntos para la interpolación.
El resultado seria mas suave aun si se usara interpolación sinusoidal en lugar de una lineal. Aquí diez puntos se utilizan para las interpolaciones:
patches/3-5-1-3-wavgorithm+sin.pd
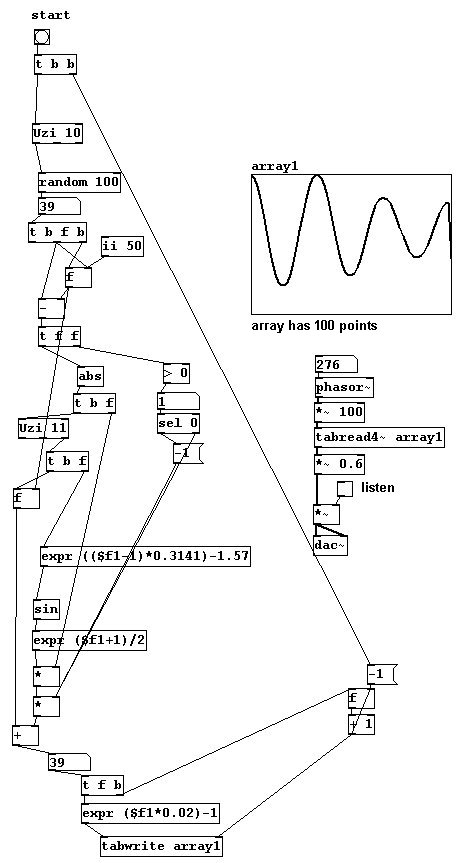
Ahora la conexión entre el final del periodo y su comienzo también debe ser interpolada. Usaremos `windowing` para esto y programaremos los calculos en un subpatch.
patches/3-5-1-3-wavgorithm+sin+fenster.pd
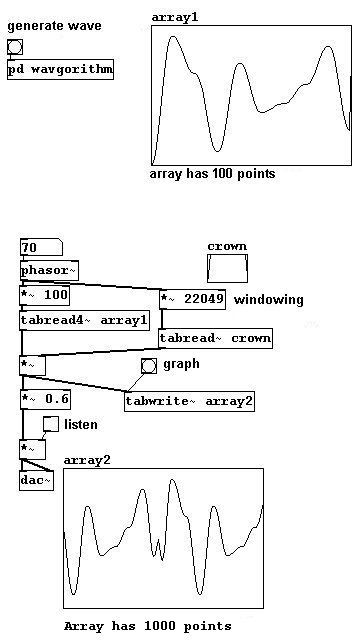
De esta forma la membrana esta en 0 al principio y al final de cada periodo. El resultado podría ser mas suave si fuera `windowed` con un window Hanning (3.9.4.1).
Ademas, funciones de transferencia usando formas de onda conocidas – por ej., cuadrada, que intensificara los parciales impares – también es posible.
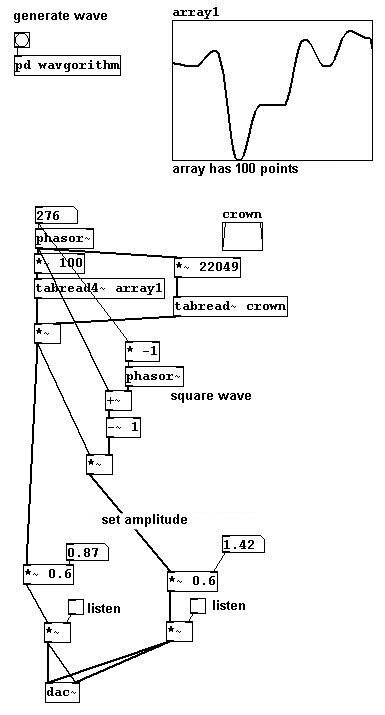
Y así. En estos últimos ejemplos, la onda debe ser creada en el control level; en contraste con los primeros ejemplos de funcion de transferencia, no podemos cambiar esto “en vivo”.
Una tecnica final que puede considerarse síntesis wave shaping es “wave-stealing”(= robo de onda). Esto requiere la toma de una pequeña sección de piezas musicales conocidas...
patches/3-5-1-4-wavestealing.pd
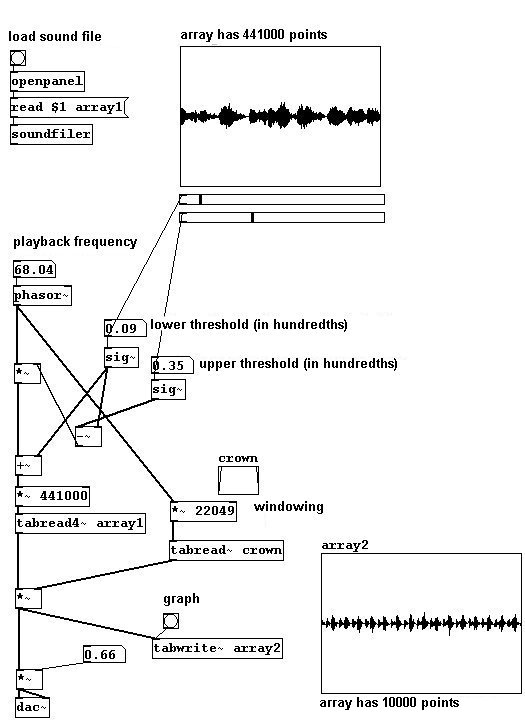
Con el siguiente patch es posible grabar formas de onda con un micrófono para cantar formas de onda.
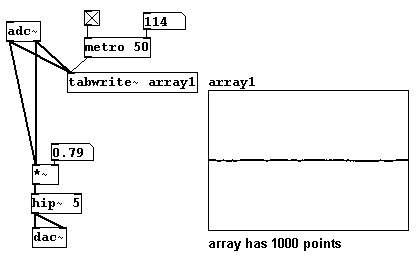
Las vocales (pronunciación Alemán) se ven algo como asi:
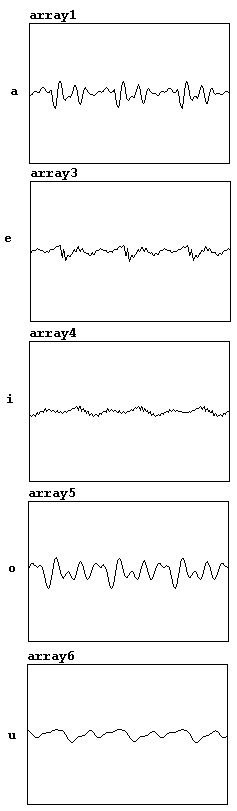
Y esta señal de entrada puede, naturalmente, también ser enviada a través de una función de transferencia:
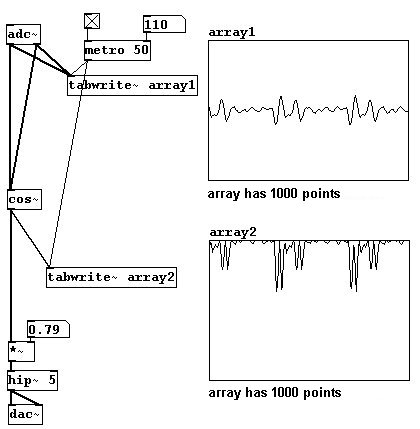
También puede dividir una onda serrucho en parciales par e impar. Para esto se necesita “wrap~”. Calcula la diferencia entre el numero de entrada y el integro mas cercano por debajo de el (se toma el valor absoluto, entonces el resultado siempre sera positivo). Algunos ejemplos chicos:
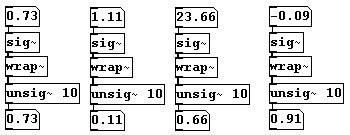
Y para la subdivisión de de la onda serrucho: el objeto “wrap~” se usa para desfasar la onda serrucho; esto luego se suma y se resta de la onda original, resultando en una onda serrucho del doble de la frecuencia y una onda cuadrada.
patches/3-5-2-3-even-odd-partials.pd
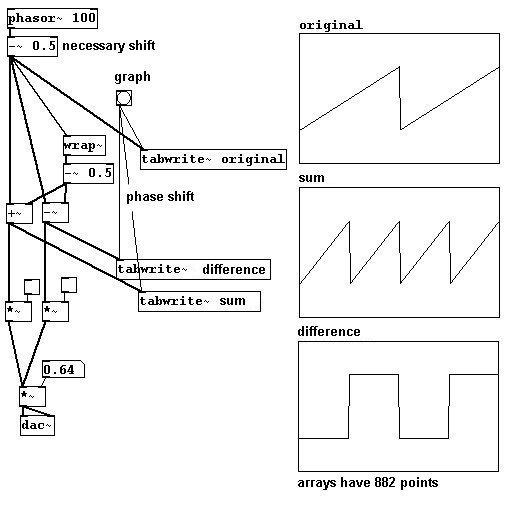
A estas alturas debe mencionarse un problema particular en procesamiento digital de sonido: foldover. Primero examinemos esta situación:
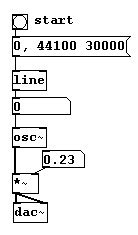
?Que sucede? Luego de los 22050 Hz, la dirección cambia hasta llegar a los 44100 Hz, en este punto tenemos una frecuencia de 0 Hz (luego, la altura volverá a subir). La razón de esto es que una frecuencia de sampleo de 44100 Hz puede producir una onda de 22050 Hz como máximo (cf. 3.1.1.3.1). Ademas hay algunos errores de lectura típicos. Miremos estas tres diferentes frecuencias: arriba una frecuencia de 11025 Hz, al medio 22050, y abajo un poco mas de 22050. Las marcas son puntos de referencia (de los samples), que tienen una velocidad constante de 44100 por segundo.
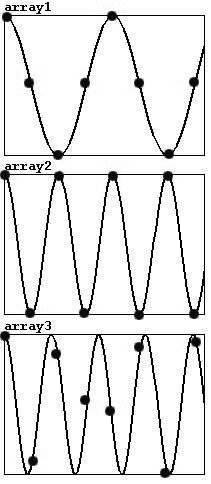
Cada periodo de una onda de 11025 Hz puede ser representada con cuatro puntos (por supuesto, la forma característica de un onda sinusoidal se pierde). 22050 Hz es la frecuencia mas alta que puede ser representada, el teorema de Nyquist requiere al menos dos puntos por periodo. Ocurrirán errores con frecuencias mas altas que esta; no todos los periodos serán capturados y los puntos de medición en realidad grabaran una frecuencia mas baja en lugar de una mas alta.
El problema se hace mas pronunciado para formas de onda que exhiban sobretonos, por ej., pulso:
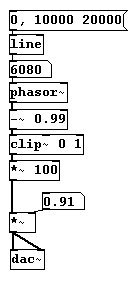
Aquí el efecto se puede notar mucho antes: luego de 700 Hz algunos sobretodos son capturados imprecisamente. Esto es por que la forma de onda pulso prácticamente consiste en tan solo una linea, que rápidamente se `pierde`. Una solución a este problema es comenzar con una forma de onda pulso, y extender la onda a medida que la frecuencia aumenta, de forma tal que se termina en una onda sinusoidal al final: